Quand on parle IA, le réseau de neurones et les LLM (Large Language Models) sont les premières technologies qui viennent dans la conversation car ils sont une tentative de reproduire à l’échelle du silicium le fonctionnement de notre cerveau pour l’un et l’apparence d’une discussion sensée pour l’autre. C’est le dernier truc à la mode et comme nous restons de grands enfants, cela a quelque chose de magique.
Cependant, il existe de nombreux autres modèles (plus mathématiques/statistiques) bien plus simples, moins tape-à-l’oeil et souvent largement suffisants pour répondre à des questions sans lancer des fermes de serveurs à plusieurs mégaWatts pour un gain relatif nul ou insignifiant (il faudrait probablement inventer le SMR et l’ASMR pour l’IA, on aurait des surprises). Par contre, cela nécessite de mobiliser son propre cerveau et faire confiance à l’intelligence… humaine… au moins au début du projet.
Il n’en est pas moins que le réseau de neurones a tout à fait sa pertinence dans certaines résolutions de problèmes (LLM beaucoup moins) et nous le verrons donc plus tard. Alors GO, vulgarisons la lowtech !
Dans le cadre de cet article, nous allons étudier un indicateur courant en médecine : l’indice de masse corporelle.
La formule : un calcul universel
De nos jours, l’IMC est un indice simple pour évaluer l’adéquation poids/taille d’un patient.
Nous pouvons décrire l’indice de masse corporelle alors que nous recueillons le poids et la taille. Celui-ci étant une application directe d’une formule mathématique, il n’y a plus aujourd’hui aucun aléa dans sa définition (même si elle fut définie empiriquement) :
IMC = POIDS / (TAILLE ^2)
(avec taille en m et poids en kg)
En R nous pouvons écrire une fonction :
# Version la plus minimale possible (à part les parenthèses
# autour de la taille qui sont là pour la lisibilité) :
imc <- \(poids, taille) poids/(taille^2)
> imc(90, 1.80)
[1] 27.77778C’est un calcul déterministe : pour un poids et une taille donnés, le résultat est toujours identique.
Par contre, l’interprétation générale du résultat de cette formule n’est pertinente que sur une portion du domaine : les poids et tailles humains entre 18 et 65 ans. Cela signifie qu’en dehors de cet intervalle l’indice est toujours calculable mais sa pertinence n’est plus au rendez-vous
La classification : interpréter la valeur
L’IMC brut n’est pas toujours parlant. Pour être utile, il est converti en catégories (pour l’adulte):
- < 18,5 : sous-poids
- 18,5 – 24,9 : normal
- 25 – 29,9 : surpoids
- 30 – 39,9 : obésité
- ≥ 40 : obésité morbide
Ces seuils proviennent d’analyses épidémiologiques. Ici encore, tout est déterministe : un IMC de 27 sera par exemple toujours classé « surpoids ».
Il est facile d’écrire cette fonction en R en utilisant cut() :
classification_obesite <- \(imc) cut(imc,
c(0, 18.5, 25, 30, 40, Inf),
c("Sous-poids", "Normal", "Surpoids", "Obésité", "Obésité morbide"))
> classification_obesite(imc(90, 1.80))
[1] Surpoids
Levels: Sous-poids Normal Surpoids Obésité Obésité morbide
# Ces fonctions sont vectorisées. Il est donc possible
# si on a des POIDS et TAILLEs dans un data.frame `donnees` de faire :
# en R de base :
> donnees$imc <- imc(donnees$POIDS, donnees$TAILLE)
> donnees$statut <- classification_obesite(donnees$imc)
# ou en dplyr :
> donnees <- donnees %>% mutate(imc = imc(POIDS, TAILLE),
statut = classification_obesite(imc))On voit ici comment une valeur continue devient une donnée catégorielle, plus directement utilisable en pratique clinique ou épidémiologique.
Je n’ose même pas mesurer le temps d’exécution d’un tel enchainement de fonctions tellement c’est dérisoire.
L’approximation : combler les trous
Chez l’adulte, l’IMC cible -nous l’avons dit- est fixe à 25.
Chez l’enfant et l’adolescent, la situation est différente : la corpulence varie selon l’âge et le sexe, ce qui impose de se référer aux courbes officielles de corpulence utilisées dans le carnet de santé.
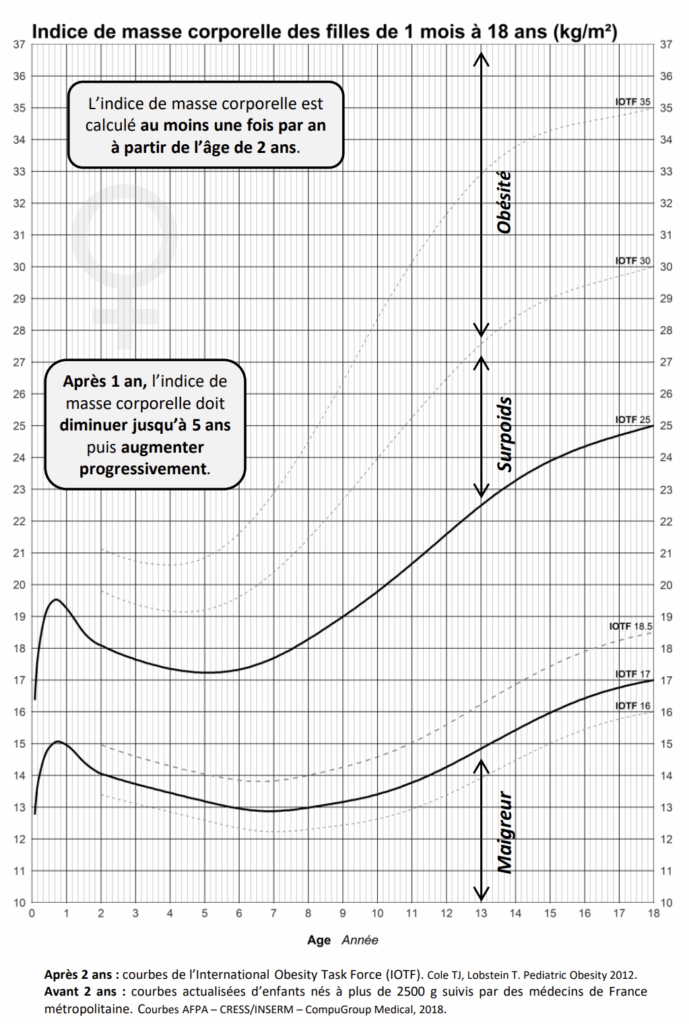
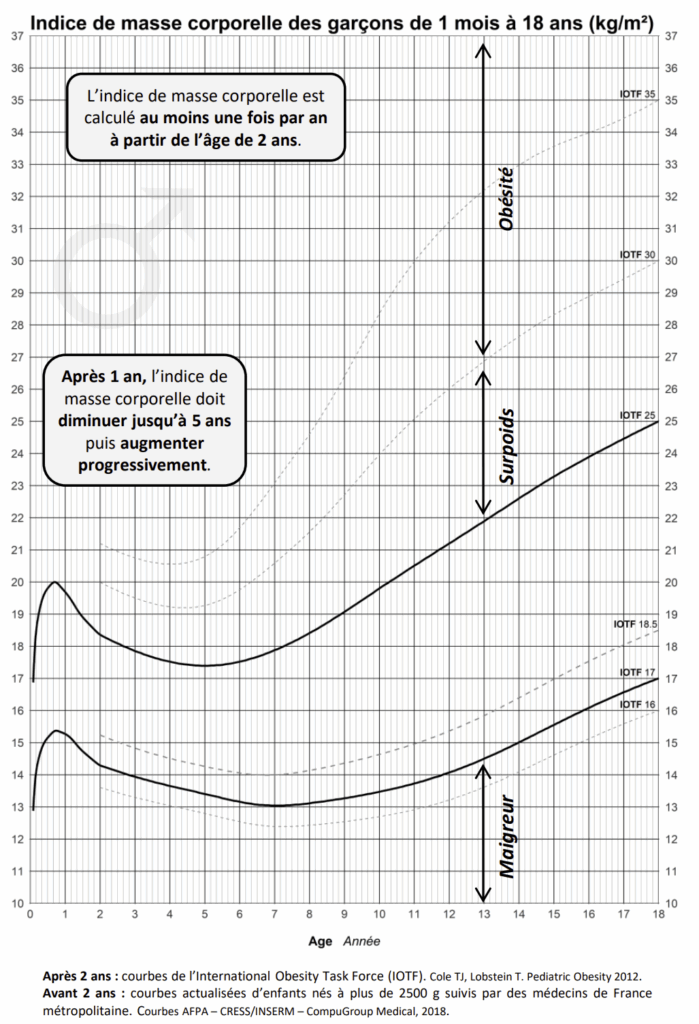
(Ces courbes sont prises du site de l’AFPA)
Suite à lecture graphique on peut obtenir quelques valeurs clés (un peu approximatives mais le but est d’illustrer) :
ref_data <- data.frame(
age = 0:18,
garcons = c(17, 19.6, 18.4, 17.9, 17.5,
17.4, 17.5, 17.9, 18.4, 19,
19.9, 20.5, 21.2, 21.9, 22.6,
23.2, 23.9, 24.5, 25),
filles = c(16.4, 19.2, 18.1, 17.7, 17.4,
17.2, 17.4, 17.8, 18.3, 19,
19?8, 20.7, 21.6, 22.5, 23.2,
23.9, 24.3, 24.8, 25)
)Mais comment savoir l’IMC à 9 ans et demi ?
Partant de ce dataframe contenant des points dont on connait la valeur, il suffit de demander à approx() les valeurs pour des points intercalaires. Elle vous retournera une approximation linéaire du résultat.
> approx(x = ref_data$age, y = ref_data$garcons, xout = c(9.5,6.3,18.5))
$x
[1] 9.5 6.3 18.5
$y
[1] 19.45 17.62 NAapprox() a calculé l’approximation linéaire pour 9 ans et demi, 6 ans et 4 mois (environ) mais n’a pas pu donner de résultat pour 18 ans et demi qui n’est pas dans l’intervalle connu (il y a une paramètre pour forcer le calcul si besoin mais ce n’est pas notre propos).
En quelques sorte, approx() a retourné la valeur se trouvant sur la courbe des garçons ci-dessous :
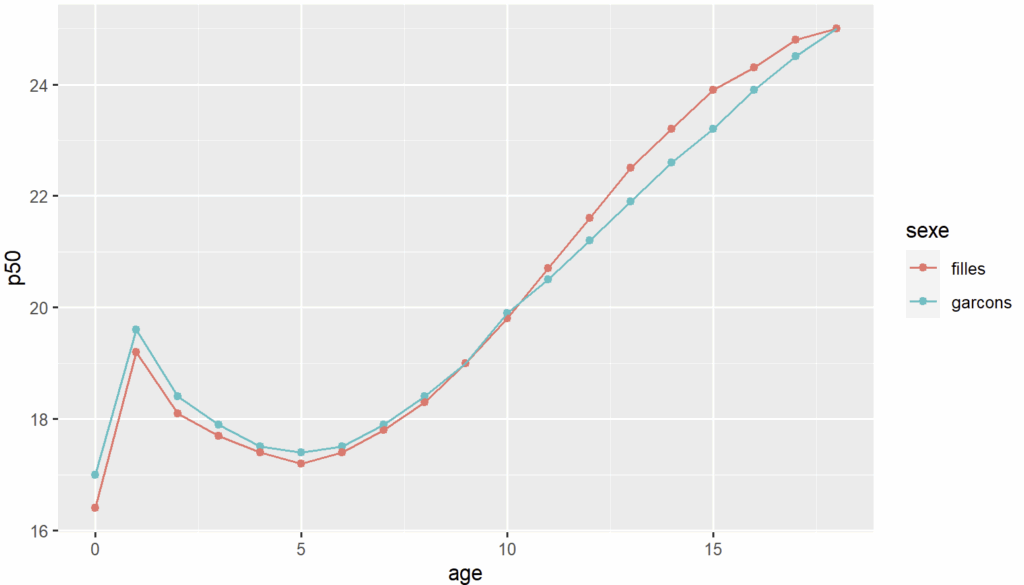
Il existe aussi une version lissée d’approx() sous la dénomination spline() qui peut être plus approchante selon les cas :
> > spline(x = ref_data$age, y = ref_data$garcons, xout = c(9.5,6.3,18.5))
$x
[1] 9.5 6.3 18.5
$y
[1] 19.45415 17.59249 25.21956Enfin il est possible d’utiliser approxfun() (ou splinefun())pour générer une fonction réutilisable qui retourne un vecteur de même longueur :
imc_garcons_approx <- approxfun(x = ref_data$age, y = ref_data$garcons)
> > imc_garcons_approx(c(9.5,6.3,18.5))
[1] 19.45 17.62 NAComme d’habitude, vous pouvez aller consulter la page d’aide de ces fonctions pour les finesses, comme le comportement en dehors des bornes, ou générer des « marches d’escalier » avec approx(..., method = "constant")).
En utilisant l’approximation, on a ainsi estimé une valeur manquante à partir des données connues.
C’est un pas de plus : on n’applique plus seulement une formule, on reconstruit une information.
L’optimisation : chercher un résultat remarquable.
Chez l’enfant, la courbe d’IMC suit un profil particulier : elle diminue progressivement passés les premiers mois après la naissance, atteint un minimum physiologique vers 5–7 ans, puis remonte ensuite.
Ce point de minimum est appelé rebond d’adiposité.
- Sur le plan mathématique, c’est un problème d’optimisation : trouver l’âge où l’IMC est minimal (un minimum local d’une courbe).
- Sur le plan clinique, l’âge de ce rebond est important :
- un rebond précoce (avant 5 ans) est associé à un risque accru d’obésité à l’adolescence et à l’âge adulte,
- un rebond plus tardif correspond au développement attendu.
Ainsi, l’optimisation illustre comment un outil statistique (courbes IMC de référence) permet d’extraire une information de santé essentielle.
Recherchons quand a lieu ce rebond chez les garçons. Pour cela nous allons utiliser optim() qui comme son nom l’indique cherche un optimum, c’est à dire le point où le résultat est minimum.
optim() a besoin non pas de points mais d’une fonction pour travailler. Ca tombe bien nous en avons crée une dans le chapitre précédent : imc_garcons_approx(). optim() a aussi besoin d’un intervalle de recherche (lower=, upper=) et d’une valeur de départ (par=). La méthode (method=) permet de choisir le mécanisme de recherche parmi ceux disponibles, ici nous prenons « Brent » (si vous êtes curieux, l’algorithme est décrit sur Wikipédia).
> res <- optim(par = 18, fn = imc_garcons_approx, method = "Brent", lower = 0, upper = 18)
> res
$par
[1] 5
$value
[1] 17.4
$counts
function gradient
NA NA
$convergence
[1] 0
$message
NULL
Le résultat de l’appel d’optim() est une liste dont il faut extraire ce qui nous intéresse. On trouve la valeur cible dans $par, et la valeur résultante (c’est à dire fn($par)) dans $value. Pour « Brent », $convergence est toujours 0 sinon c’est une sorte de code d’erreur si le résultat n’est pas l’optimum. $counts contient le nombre d’itération. Après l’appel à optim() on récupère donc res$par.
Dans notre cas, notre recherche nous dit donc que l’âge masculin moyen du rebond d’adiposité est 5 ans. Si nous avons un garçon dont la courbe rebondit avant cet âge alors il a probablement besoin d’un peu plus de suivi médical et diététique.
Pour faire un parallèle avec Microsoft Excel, on peut dire que optim() est en quelque sorte la fonctionnalité solveur du logiciel tableur en mieux.
Si vous cherchez l’aide de R, vous allez trouver que, dans notre configuration, optim() utilise en fait une autre fonction qui ferait exactement la même chose : optimize(). Vous pouvez bien sûr directement l’utiliser. Mais optimize() est univariée (ne traite qu’une relation 1 variable vers 1 résultat) alors qu’en utilisant une autre méthode que Brent, il est possible d’utiliser optim() de façon plus polyvalente en multivariée (chercher un optimum en faisant varier plusieurs paramètres). J’ai donc tendance à toujours utiliser optim(), cela m’évite de me mélanger dans les paramètres…
La modélisation : accepter l’incertitude
Enfin, la corpulence d’un individu ne dépend pas seulement de son poids et de sa taille. Elle est influencée par l’âge, le sexe, les habitudes alimentaires, les comorbidités, etc.
On entre alors dans le domaine des modèles statistiques.
L’exemple le plus classique est la régression linéaire : relier une variable réponse (par ex. durée de séjour) à un ou plusieurs prédicteurs (IMC, âge, pathologies associées).
Mais nous le verrons dans le prochain article car c’est un gros morceau (et pour le coup, nous quitterons la clinique et l’étude de l’IMC pour retourner faire de l’étude de données PMSI).
Conclusion
Nous avons donc vu dans cet article des façons simples et peu couteuses d’utiliser la puissance de l’ordinateur afin d’obtenir des réponses plus ou moins précises à des questions sur :
- un jeu de données mathématiquement descriptible : en créant une fonction de calcul donnant un résultat numérique
- une interprétation qualitative de ce résultat par l’utilisation d’une fonction de classification
- la recherche de données pour des paramètres n’existant pas dans le jeu de données source avec l’approximation
- la découverte de points remarquables par la recherche d’un optimum local
Toutes ces actions n’ont pas nécessité d’entrainement informatique mais qu’un statisticien du 18e siècle constate une particularité du jeu de données, cherche une formule mathématique suffisamment adaptée à celle-ci puis à leur interprétation, qu’un opérateur actuel valide la pertinence de la fonction d’approximation et vérifie que l’optimum trouvé ait un sens. C’est en quelque sorte une intelligence collective à travers les siècles.
Encore une chose
Cet article en lui-même est fini, cependant je ne voudrais pas vous priver d’un peu d’histoire et de lecture complémentaire.
L’IMC est un indice qui a été redécouvert dans la 2ème partie du 20e siecle. A l’origine, il est évoqué par Alphonse Quetelet (on l’appelait d’ailleurs historiquement Indice de Quetelet) en 1832 comme un élément conclusif parmi d’autres d’un article « Recherches sur le poids de l’homme aux différens âges » (faites vous plaisir, la publication initiale est disponible en ligne sur Persee 1, je trouve sa lecture rafraichissante de simplicité de la démarche et de tournures surannées) :

Ce qui veut dire qu’il existe une proportion constante (a) entre poids et carré des tailles chez les adultes :
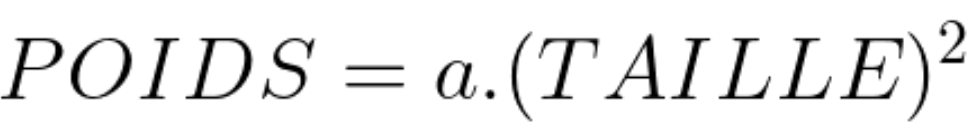
et donc que :
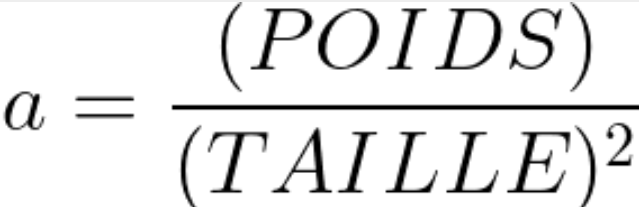
et au final, ce a est en fait notre IMC.
Si vous avez lu l’article sur les formules, vous me voyez venir avec mes gros sabots. Cela s’écrit dans cette notation :
# LA formule qui met en relation le poids "idéal" et du carré de la taille :
POIDS ~ I(TAILLE^2)
# ou si on considère l'IMC uniquement sur son intervalle où il est constant
IMC ~ POIDS + I(TAILLE^2)
# Maintenant si on veut généraliser
# alors on a vu plus haut que le sexe et age jouent un rôle
# au moins chez l'enfant donc il faut aussi les ajouter
# comme variables indépendantes et les avoir dans le jeu de données :
POIDS ~ I(TAILLE^2) + SEXE + AGE
# ou
IMC ~ POIDS + I(TAILLE^2) + SEXE + AGEEn vous basant là dessus et sur le prochain article sur les modèles, je pense que vous pourrez jouer à Quetelet comme en 1832 et faire les études qui ont dû lui prendre des semaines voire des mois en quelques dizaines de minutes, il vous suffira juste de trouver un jeu de données pertinent et non biaisé. Merci R et les statistiques modernes !
Un dernier point :
L’IMC étant tiré d’une modélisation de séries d’observations du 19è siècle, il possède ses limites (en particulier en terme d’adaptabilité aux âges extrêmes de la vie et à la société moderne, 2 siècles et l’invention des fast-food plus tard). Dans cette optique plusieurs tentatives pour le revisiter voire le remplacer ont vu le jour, pour le moment sans le même succès. L’avenir nous dira si l’IMC fêtera son 200è anniversaire…
- Quételet A. Recherches sur le poids de l’homme aux différens âges. In: Nouveaux mémoires de l’Académie royale des sciences et belles-lettres de Bruxelles. Tome 7, 1832. pp. 1-44.
DOI : https://doi.org/10.3406/marb.1832.2745 ↩︎

