Nous avons vu la fois précédente la création de points.
Cette fois-ci nous aborderons les graphiques en barre, souvent (et parfois à tort) appelés histogrammes.
Avant tout l’élément graphique de base : le rectangle !
Un rectangle est un élément dessiné dans un repère. Il se définit par exemple par un coin inférieur et un coin supérieur. Ggplot dispose d’une telle primitive vectorisable sous forme de la fonction geom_rect() mais aussi de dérivées.
Son prototype attend des vecteurs de coordonnées :
xminetymin(obligatoires)xmaxetymax(par défaut leur valeur est respectivement dexmin+1etymin+1)
Il existe une autre fonction apparentée appelée geom_tile() dont les paramètres xmin / ymin et xmax / ymax sont remplacés par les paramètres x / width et y / height. Le calcul de transformation étant :
x = (xmin + xmax) / 2y = (ymin + ymax) / 2width = xmax - xmin(valeur par défaut 1)height = ymax - ymin(valeur par défaut 1)
Enfin, il existe une 3ème version, geom_raster() qui est une version optimisée dessinant toujours des rectangles de même width et height . Elle est utilisée par exemple pour dessiner des heatmaps (que nous verrons une autre fois).
Vous comprenez bien en parcourant les paragraphes ci-dessus que cette fonction manipule des valeurs continues pour chaque coordonnée et n’est pas adaptée pour des valeurs discrètes.
On peut éventuellement utiliser de telles fonctions pour dessiner des éléments englobants. Exemple avec notre jeu de données restreint :
library(dplyr)
library(ggplot2)
library(readr)
RSA <- read_delim("extrait_RSA.csv",
delim = ";",
escape_double = FALSE,
trim_ws = TRUE)Nous cherchons à représenter les extrêmes de durées de séjour en fonction de l’âge du patient et de la sévérité/CMA.
# Restraignons un peu pour améliorer la lecture, par exemple
# ici uniquement les séjours médicaux de la CMD 06
RSA <- RSA %>% filter(grepl("^06M", GHMOUT) & DS>0)
# Transformons le jeu pour ne garder que les données min max :
mRSA <- RSA %>% group_by(SEVOUT) %>% summarise(xmin = min(AGEA), ymin = min(DS), xmax = max(AGEA), ymax = max(DS))
# et nous pouvons alors le dessiner
graph = ggplot(mRSA) + geom_rect(aes(xmin = xmin, xmax = xmax, ymin = ymin, ymax = ymax, fill = SEVOUT), alpha = .5)
# Il est possible de rajouter en surimpression les points
# de données par exemple avec
graph + geom_point(data = RSA, aes(x = AGEA,y = DS, color = SEVOUT))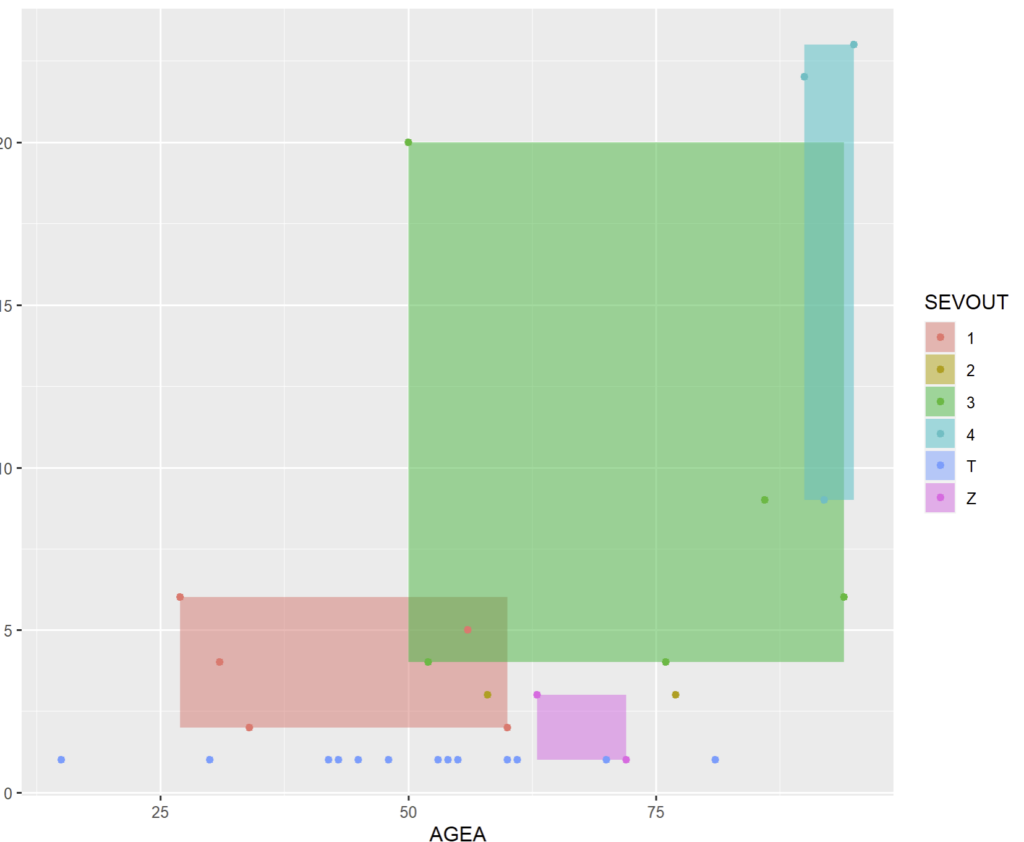
Comme d’habitude l’affichage sera plus pertinent avec des vraies données issues de votre RSA ou RSS (Il n’y a pas de rectangle pour les SEV 2 et T car le jeu de données est petit et la DS est constante).
Cela reste cependant plus cosmétique que pertinent pour l’analyse.
Un peu de théorie.
Les autres fonctions pour dessiner des rectangles telles que
geom_bar()geom_col()geom_histogram()geom_boxplot()geom_crossbar()
ne sont que des pré-paramétrages de geom_rect(), des transformations implicites des données sources et des adaptations des éléments de présentations tels que les libellés. Nous allons les passer en revue selon le type de données qu’elles requièrent et manipulent.
Des barres pour une variable discrète
Une barre est un rectangle dont une borne (ymin si y est > 0 ou ymax sinon) a toujours une valeur de 0 et les données ne se superposent pas dans un jeu de données car elles sont discrètes. geom_bar() applique la fonction statistique count(). Ainsi ;
ggplot(RSA) + geom_bar(aes(x = SEVOUT))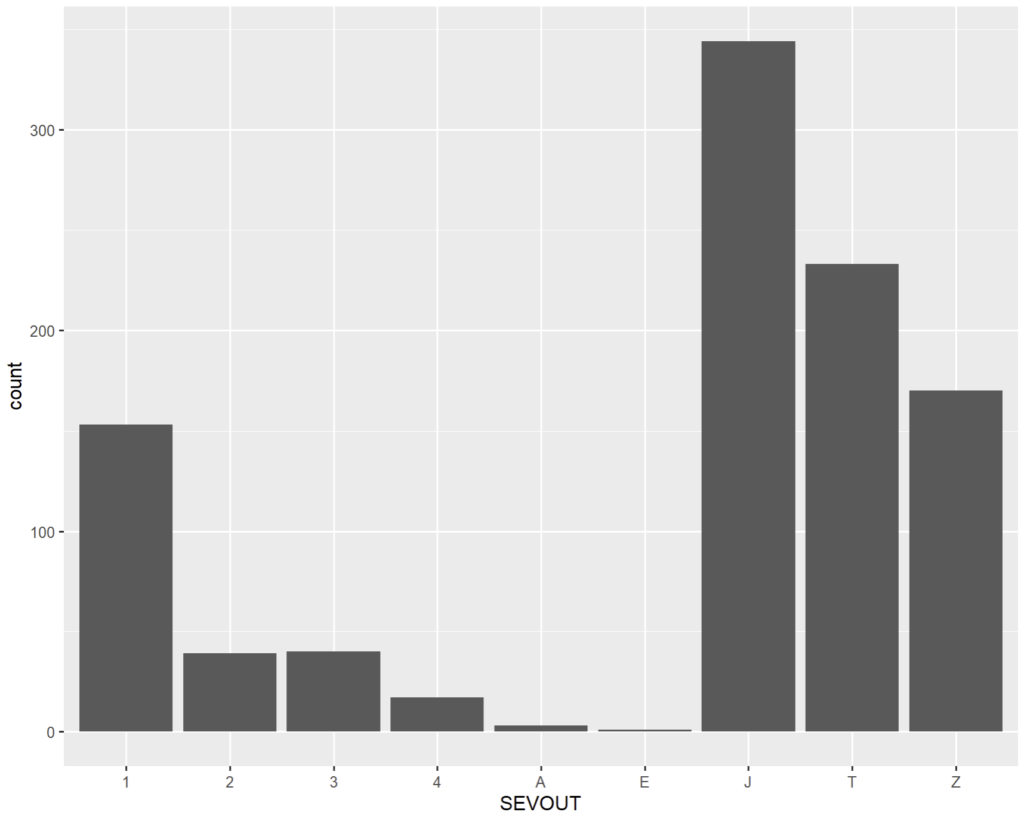
a tout de même un sacré air de ressemblance avec
RSA %>% mutate(SEVOUT = as.factor(SEVOUT)) %>%
count(SEVOUT) %>%
mutate(x = as.numeric(SEVOUT)) %>%
ggplot() +
geom_rect(aes(xmin = x - .45,
xmax = x + .45,
ymax = n),
ymin = 0)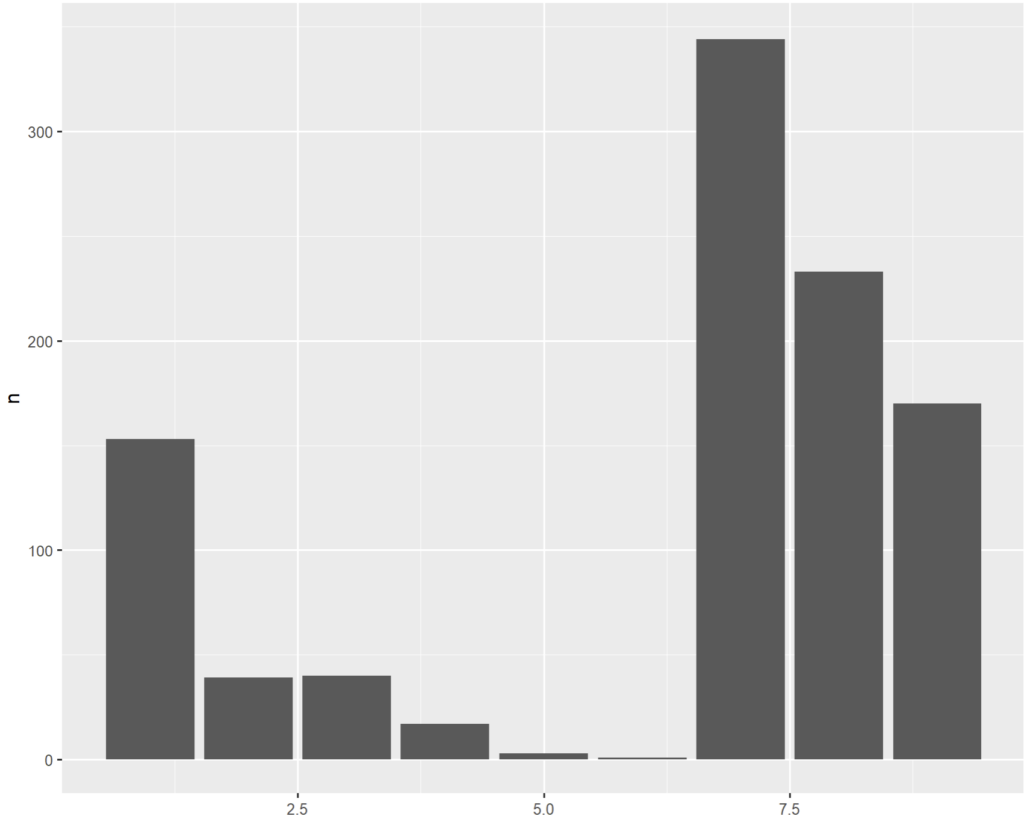
à l’exception des dénominations d’axes.
Nous avons donc geom_bar() qui nous permet dans sa version par défaut de représenter la composition d’effectif en nombre absolu d’une valeur discrète. Il n’est pas possible de passer plus d’une valeur d’axe à cette fonction (soit x comme ici, soit y si on veut un graphique horizontal).
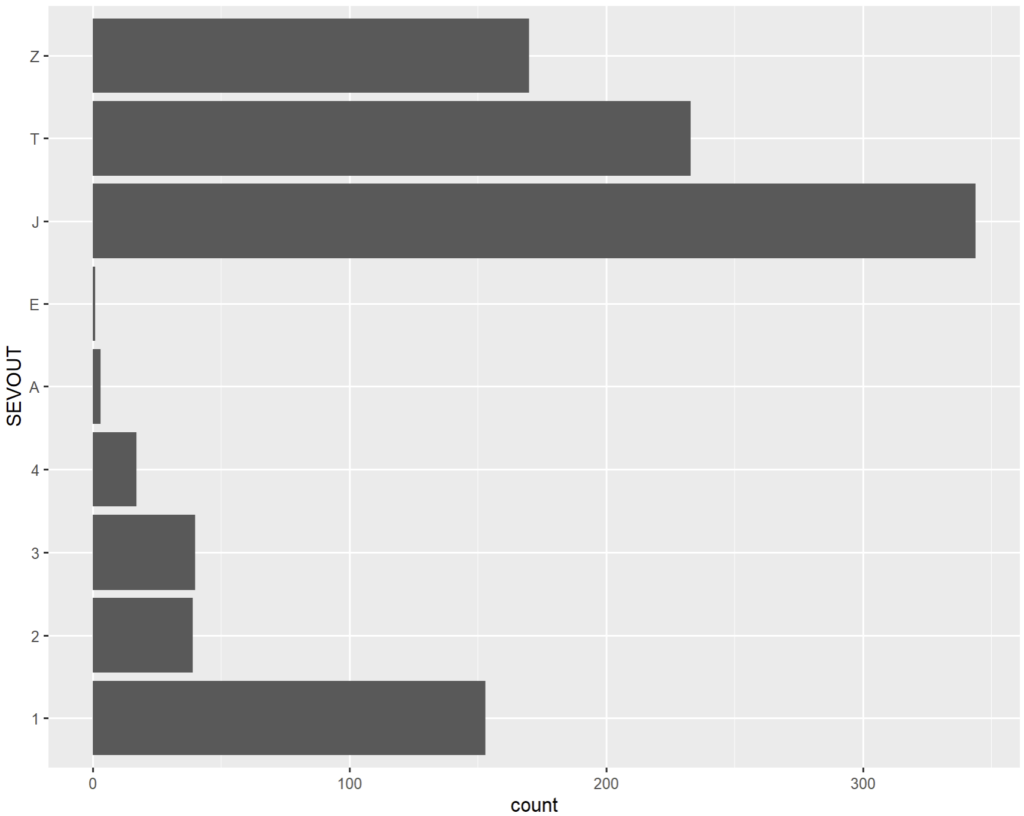
Nous pourrions par contre jouer avec les autres paramètres d’esthétique pour ajouter d’autres données. Par exemple :
#On filtre les séjours en CMD 08
ggplot(RSA %>% filter(grepl("^08",GHMOUT))) +
# et on trace un graphique par mois de sortie et les différentes sévérités empilées
geom_bar(aes(x=MOIS, fill = SEVOUT), position = "stack")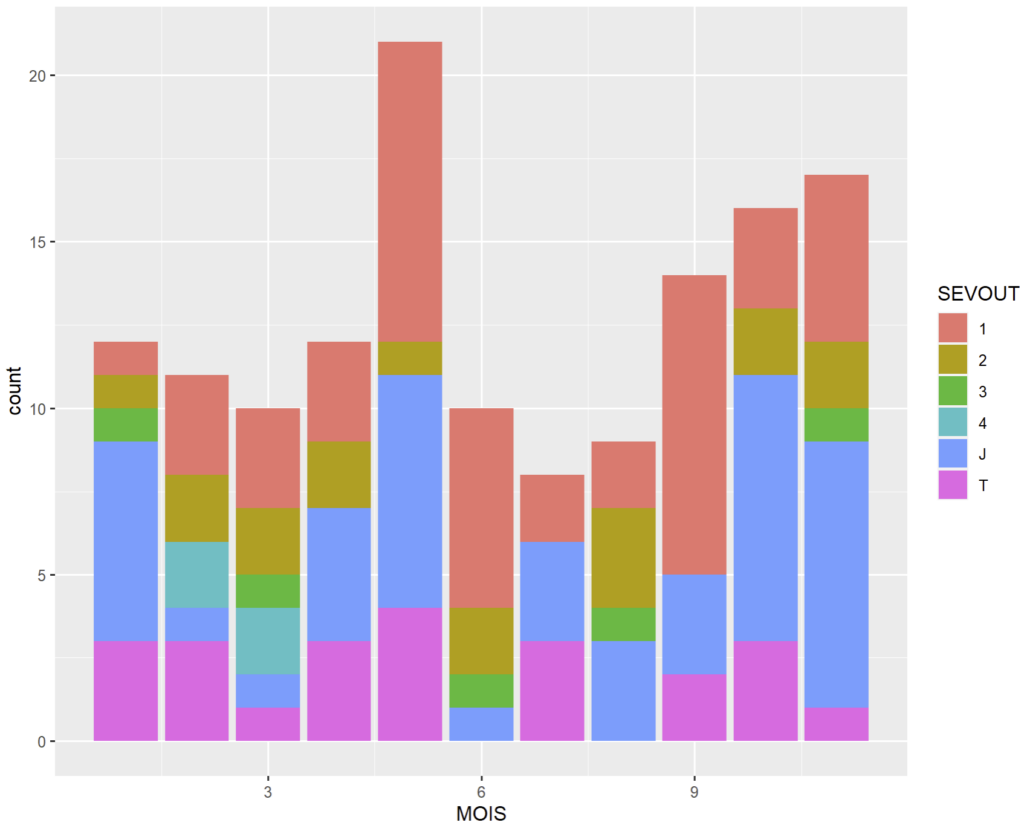
Dans cet exemple, position = "stack" (c’est la valeur par défaut aussi) demande que chaque barre soit empilée sur la précédente tant que x ne varie pas. La couleur de remplissage (fill) changeant en fonction de SEVOUT.
Nous verrons plus loin les différentes positions possibles.
Il est possible d’ajouter un autre paramètre esthétique facultatif weight servant à pondérer le décompte. La valeur implicite « y » devenant alors y(x) = sum(<<valeur du champ dont le nom a été passé a weight pour la valeur x >>) .
Malheureusement notre jeu d’exemple ne contient pas de champ pertinent pour illustrer ce fonctionnement, nous allons donc utiliser le jeu de démo diamonds.
diamonds contient plus de 50000 entrées sur des diamants. Nous pouvons donc compter les diamants par couleur via :
# décompte des diamants par couleur (variable "color")
ggplot(diamonds) + geom_bar(aes(x = color))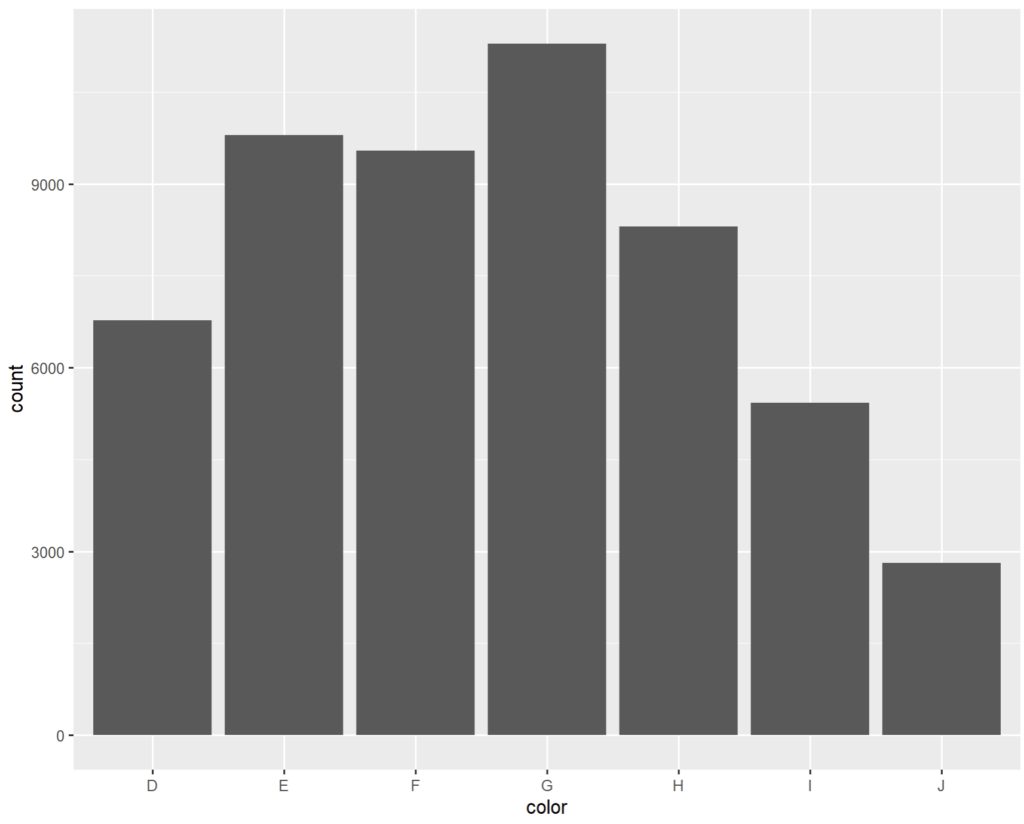
Mais nous pouvons rajouter la valeur (variable « price ») comme poids et donc obtenir une valorisation par couleur :
# valeur cumulée de tous les diamants de la base selon la couleur
ggplot(diamonds) + geom_bar(aes(x = color, weight = price))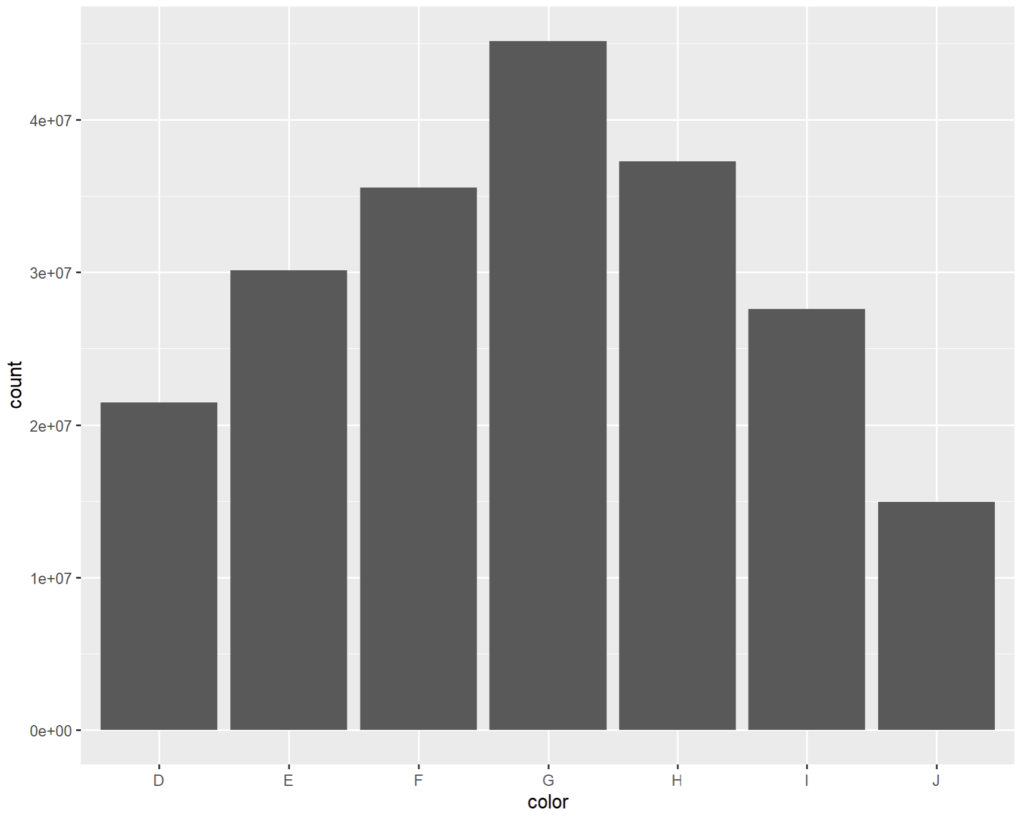
Là où cela se complique c’est si la valeur a représenter ne correspond pas à la (pseudo-)fonction y(x) = sum(weight(x)), c’est à dire que nous voulons mettre en évidence la liaison entre…
Une variable discrète et une continue
L’étape suivante après avoir introduit une pondération dans geom_bar() qui est un cas particulier, est de tracer un graphique en barre illustrant la relation entre une variable discrète (en abscisse) et une variable continue en ordonnée. Voici donc geom_col().
Notre exemple ci-dessus peut s’écrire :
# valeur cumulée de tous les diamants de la base par couleur
ggplot(diamonds) + geom_col(aes(x = color, y = price))donne à nouveau :
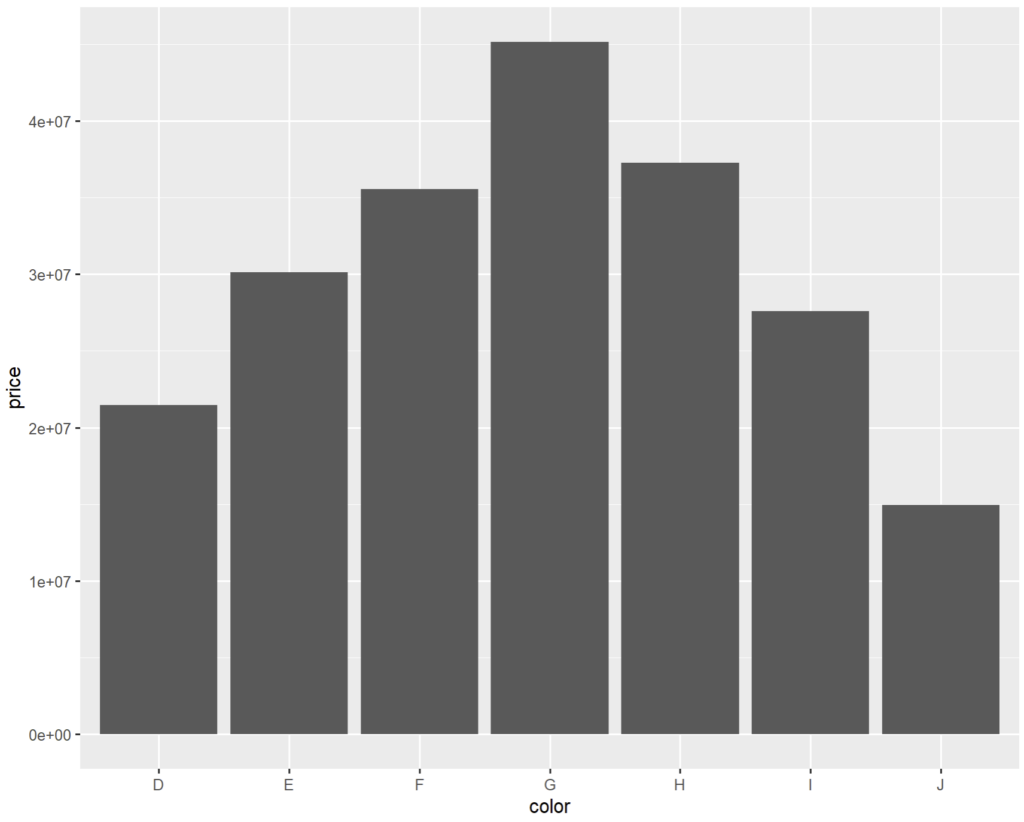
En effet, par défaut, geom_col() établit un regroupement par « x » et une sommation de « y ». Mais nous sommes libre de mettre le « y » que nous voulons et ainsi contrôler l’aspect.
Pour notre RSA, nous pourrions vouloir représenter l’âge moyen en fonction du niveau de sévérité du séjour :
# Il nous faut produire le jeu transformé
age_moyen_sev <- RSA %>% group_by(SEVOUT) %>% mutate(y = mean(AGEA, na.rm = TRUE))
age_moyen_sev
# A tibble: 9 x 2
SEVOUT y
<chr> <dbl>
1 1 63.5
2 2 75.8
3 3 79.5
4 4 74.8
5 A 52.7
6 E 93
7 J 60.7
8 T 52.8
9 Z 60.9
# Il y a bien 1 ligne par valeur de SEVOUT
# puis on appelle ggplot
ggplot(age_moyen_sev) + geom_col(aes(x = SEVOUT, y = y))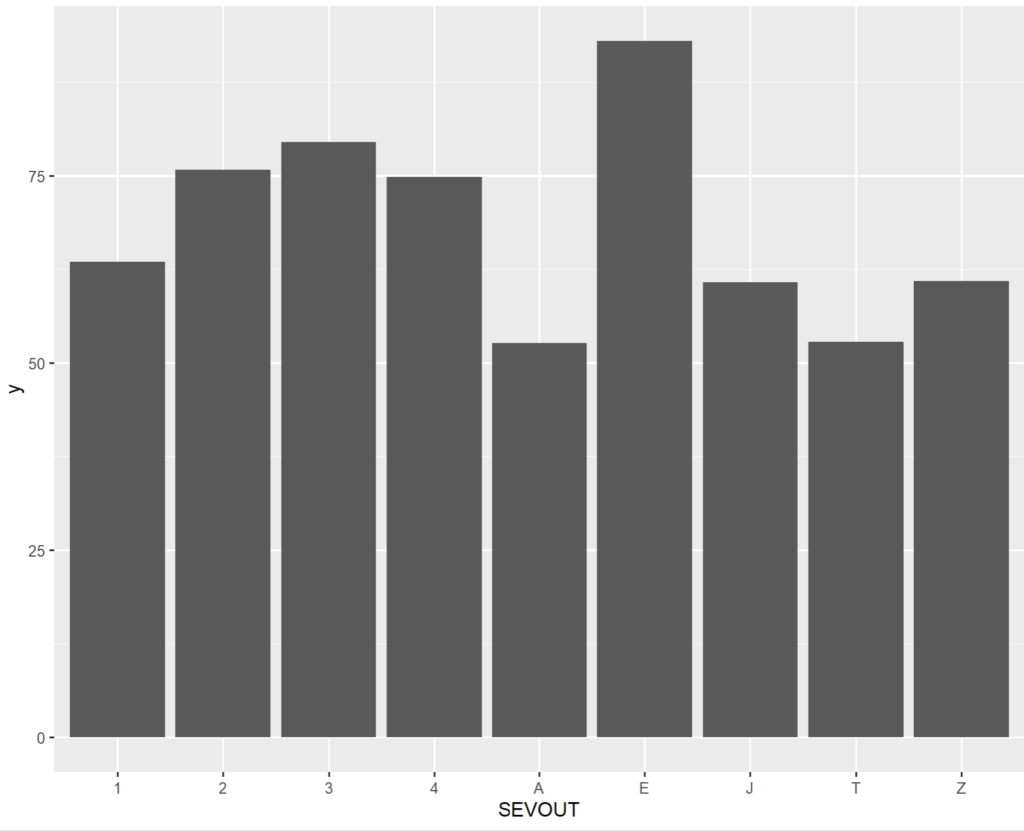
Deux variables continues
Lorsque nous avons des variables continues, le graphiques par barre n’est pas le plus pertinent pour représenter directement les valeurs car la largeur de chaque barre devrait logiquement tendre vers 0 selon la précision de la donnée. On se retrouverait alors avec une « forêt d’aiguilles » ; voici par exemple, toujours tiré du jeu diamonds, un graphique en barre cherchant à illustrer la distribution du prix des pierres :
ggplot(diamonds) + geom_bar(aes(x = price))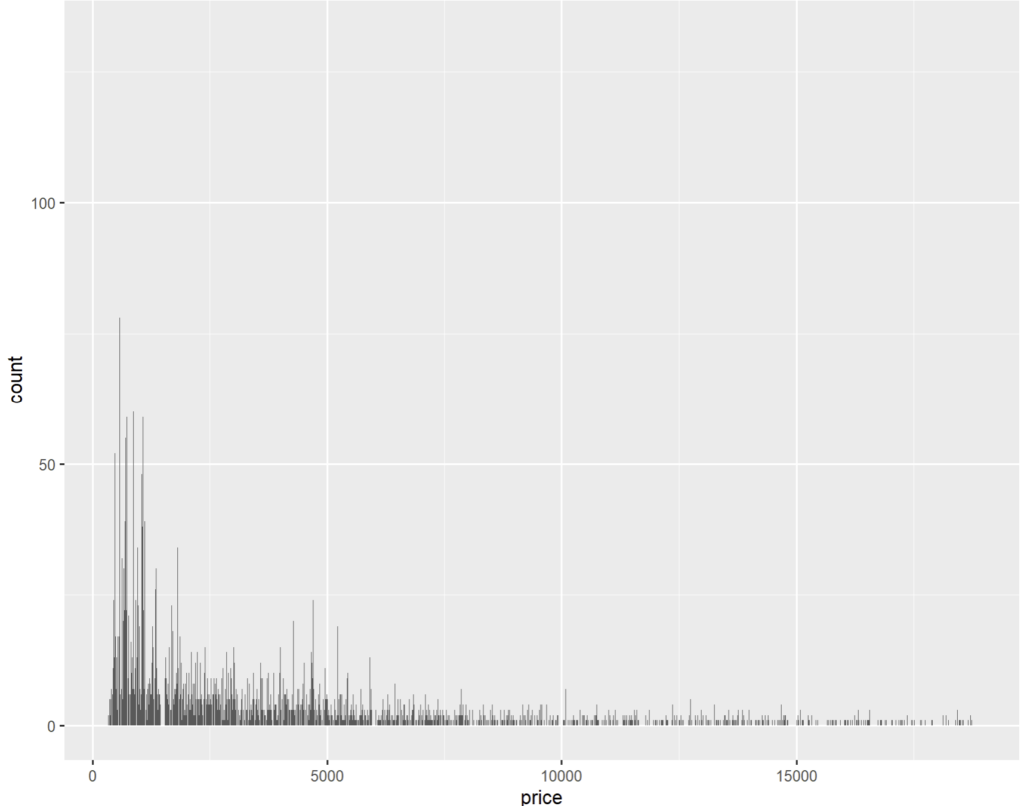
… pas très parlant… les variations de quelques centimes créent trop de valeurs individuelles en abscisse pour permettre une analyse quelconque. Il faut donc les regrouper. C’est là qu’arrive la géométrie histogramme (geom_histogram()) et les paramètres bins, binwidth et breaks.
Il s’agit dans les faits de transformer une valeur continue en valeur discrète.
D’abord sans option :
> ggplot(diamonds) + geom_histogram(aes(x = price))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
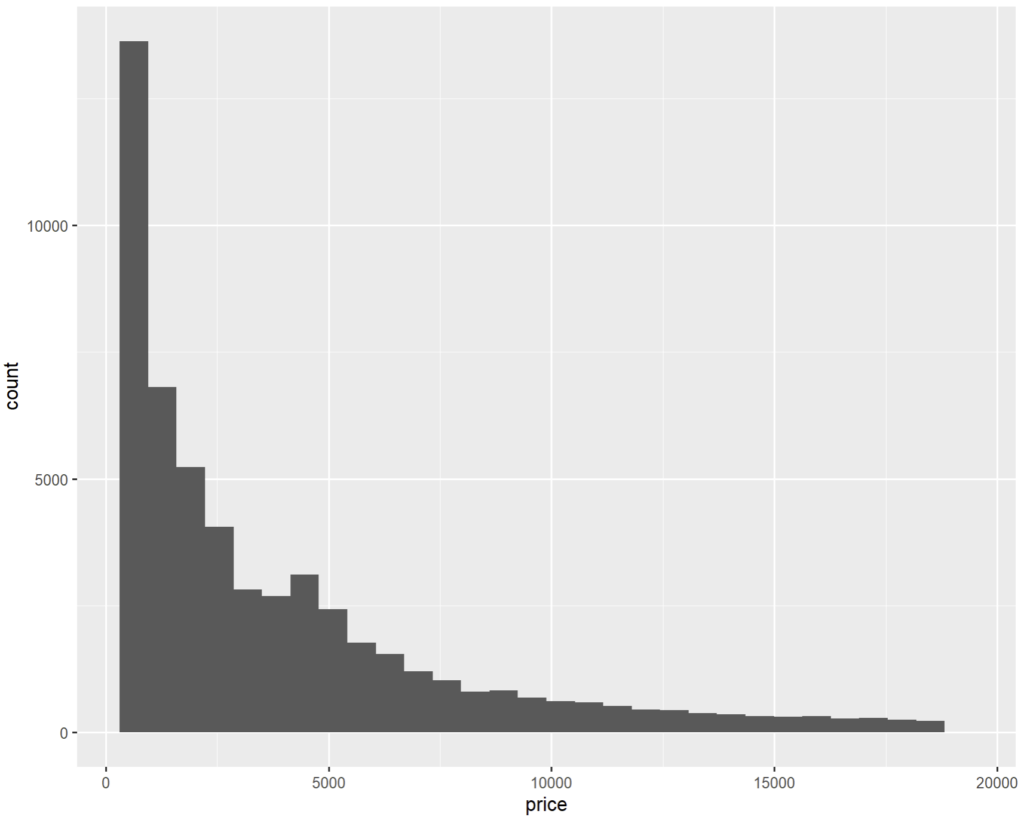
R nous précise qu’il a choisi une valeur par défaut à 30 pour bins mais qu’on peut le modifier en changeant binwidth. En fait ces 3 options sont liées ou se remplacent.
bins (paniers en anglais) fixe le nombre de barres qui seront dessinées, tandis que binwidth fixe la largeur d’un panier (dont découle leur nombre). On peut donc trouver la fonction mathématique qui lie les 2 :
# binwidth = max(x) - min(x) / <<bins>>
# et inversement
# bins = max(x) - min(x) / <<binwidth>>
ggplot(diamonds) + geom_histogram(aes(x = price), bins = 10)
# est donc équivalent à
ggplot(diamonds) + geom_histogram(aes(x = price), binwidth = (max(diamonds$price) - min(diamonds$price)) / 10)Quant à breaks, il s’agit de la définition arbitraire par l’utilisateur des limites des paniers.
Ainsi, on pourrait décider de faire des paniers plus petits dans les petites valeurs qui sont plus fréquentes :
Il est possible de définir breaks à partir de bins et binwidth mais pas l’inverse.
# breaks = seq(min(diamonds$price),max(diamonds$price),length.out = <<bins>>)
# ou
# breaks = seq(min(diamonds$price),max(diamonds$price), by = <<binwidth>>)
ggplot(diamonds) + geom_histogram(aes(x=price),breaks = seq(min(diamonds$price), max(diamonds$price), length.out = 10))
## ou donc
ggplot(diamonds) + geom_histogram(aes(x=price),breaks = seq(min(diamonds$price), max(diamonds$price), by = 1849.70))
# sont équivalents à (à quelques réglages de précision près)
ggplot(diamonds) + geom_histogram(aes(x = price), bins = 10)Quoi qu’il en soit, cela n’a souvent pas réellement de sens sans adaptation de la question qu’on cherche à illustrer.
Là où breaks a plus de sens, c’est lorsqu’il est associé à un calcul de densité car alors la surface du rectangle est proportionnelle à la fréquence des valeurs couvertes. Par exemple comparez ces études sur l’âge de la population des patients venus en CMD 08, nous ne sommes pas très intéressés par les « jeunes » (sans les ignorer totalement) et voulons regrouper les séniors de plus de 50 puis 80 ans de façon différente :
# Prenons les GHM d'appareil locomoteur
cmd_08 <- RSA %>% filter(grepl("^08",GHMOUT))
#et appliquons-leur 2 modèles d'histogramme:
#- par défaut (dénombrement brut)
ggplot(cmd_08) + geom_histogram(aes(x = AGEA, fill = ..density..), breaks = c(0, seq(50, 75,by = 5), seq(80, 100, by = 10)))
#- par fréquence (graphe de densité)
ggplot(cmd_08) + geom_histogram(aes(x = AGEA, y = ..density.., fill = ..density..), breaks = c(0, seq(50, 75,by = 5), seq(80, 100, by = 10)))
# pour rappel seq() permet de créer un vecteur d'une suite arythmétique ainsi :
c(0, seq(50, 75,by = 5), seq(80, 100, by = 10))
[1] 0 50 55 60 65 70 75 80 90 100(J’ai laissé la densité comme critère de couleur de remplissage pour que vous puissiez mieux voir la correspondance entre les 2 graphes)
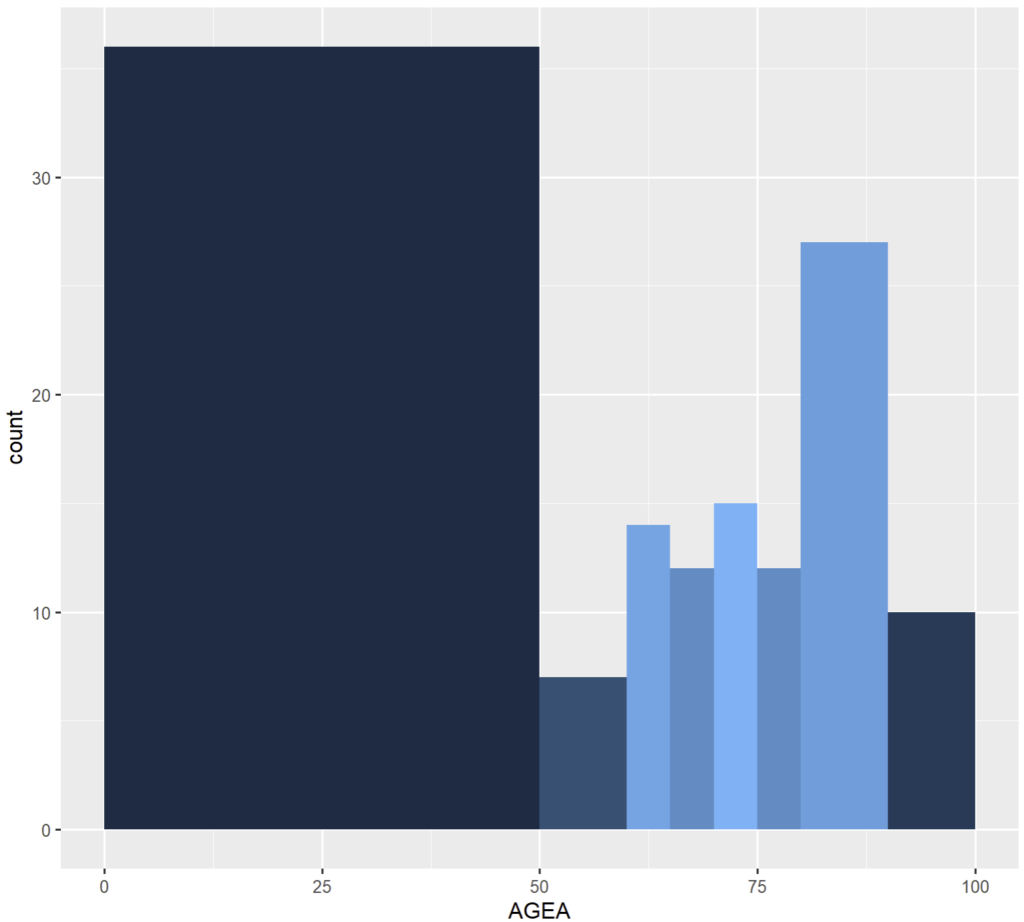
et :
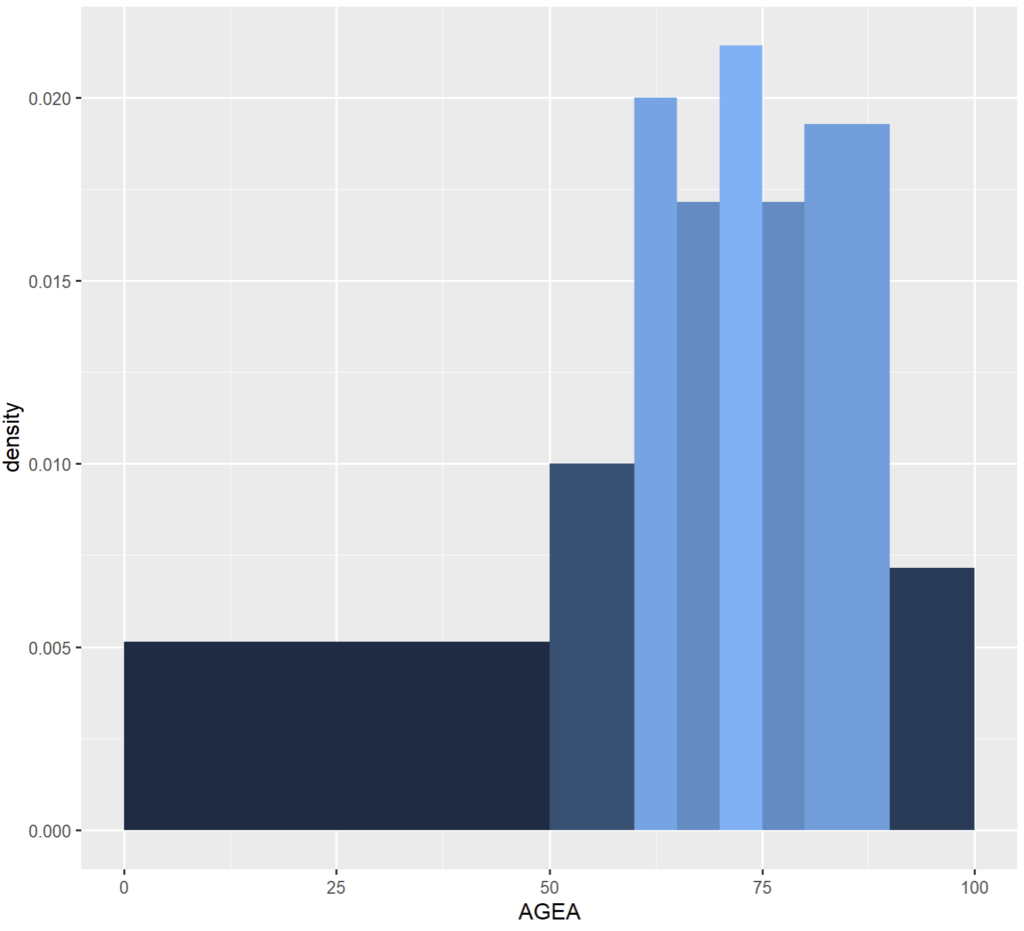
dans le premier cas, on se rend compte que, certes, il y a plus de personnes opérées entre 0 et 49 ans en nombre absolu (la fonction statistique est count(), celle par défaut) qu’entre par exemple 70 et 75 ans. Mais dans le second graphe, on s’aperçoit que la fréquence est bien supérieure dans les tranches 50-55, 55-60 et suivantes. Les données ont été normalisées selon x.
geom_boxplot() et geom_crossbar()
Je ne développerai pas ces 2 fonctions qui servent à générer des graphiques composés, c’est à dire permettant d’illustrer à moindre code, des représentations habituelles comportant -entre autres- en leur sein des rectangles.
Vous avez une illustration de geom_boxplot() dans l’article précédent pour représenter les caractéristiques statistiques principales d’un jeu de données (moyenne, médiane, écart-type, valeurs extrêmes).
Quant à geom_crossbar(), il permet de dessiner des barres depuis un jeu de données ayant des valeurs y, ymin et ymax en une seule fonction (ou y représente généralement la moyenne).
Le paramètre position
« stack »
Les graphes en barre peuvent représenter plusieurs séries de données, par exemple en rajoutant un critère secondaire comme nous l’avons vu plus haut, où la sévérité était individualisée par couleur :
ggplot(cmd_08) + geom_bar(aes(x=MOIS, fill = SEVOUT), position = "stack")
Pour empiler les barres, nous avons utilisé position = "stack" qui veut exactement dire cela. C’est d’ailleurs la valeur par défaut si position est omis.
Mais d’autres valeurs sont possibles :
« dodge »
range les barres cote à cote (dodge a plusieurs significations qui tournent autour de l’évitement)
ggplot(cmd_08) + geom_bar(aes(x=MOIS, fill = SEVOUT), position = "dodge")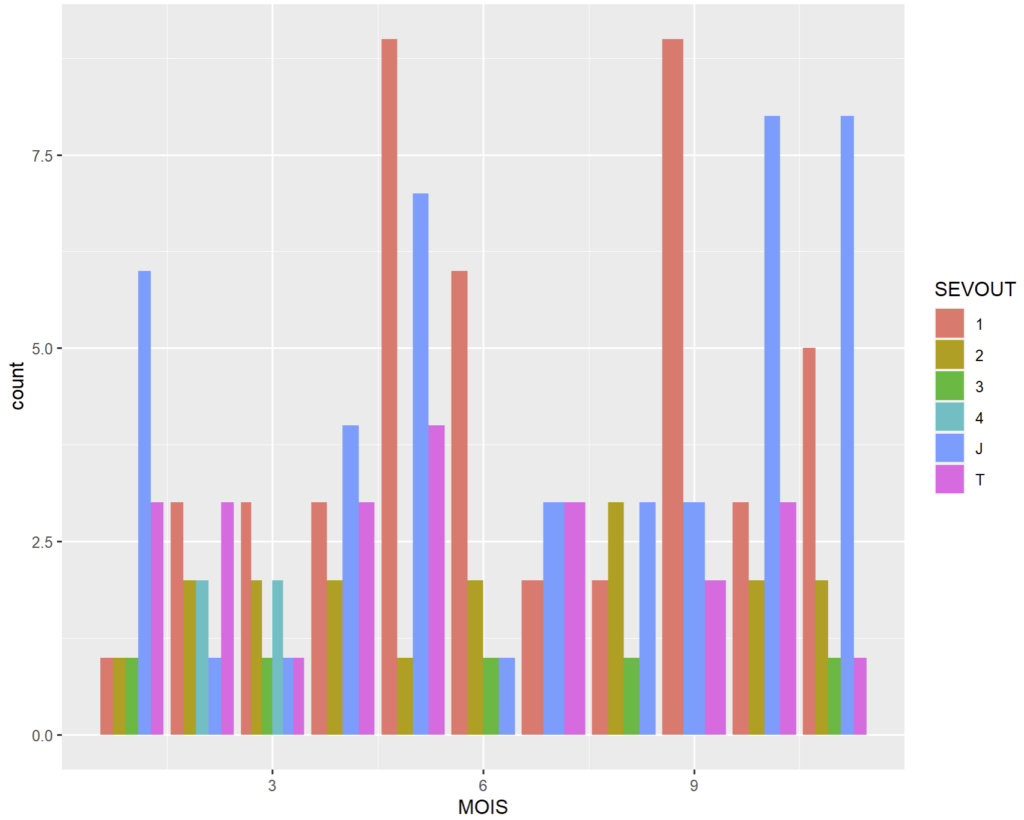
« fill »
permet d’étendre proportionnellement chaque ensemble de barre à « 1 » (100% en quelque sorte). C’est une normalisation qui permet de comparer les catégories en abscisse entre elles même si elles ont des tailles d’échantillon différents.
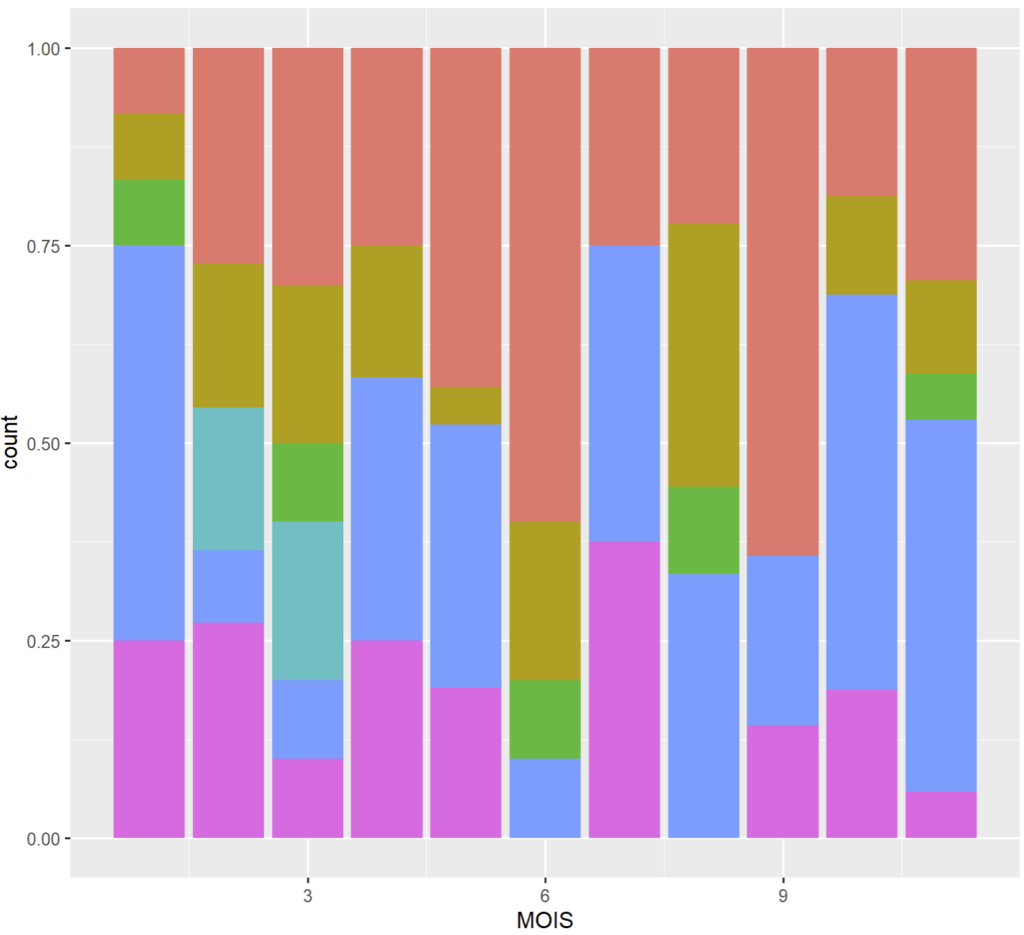
Pour les graphes en barres, les autres valeurs prédéfinies de position n’ont pas trop de sens ("jitter", "nudge", "identity"), je ne les évoquerai pas ici.
Un peu de théorie : Pourquoi utiliser des barres plutôt que des points ou des lignes
Une question que vous pouvez (et devez) vous poser est : Est-ce que je dois plutôt utiliser un graphique en barre ou des points, ou un graphique en ligne ?
En effet, l’expressivité n’est pas la même.
Prenons les 3 représentations graphiques suivantes :
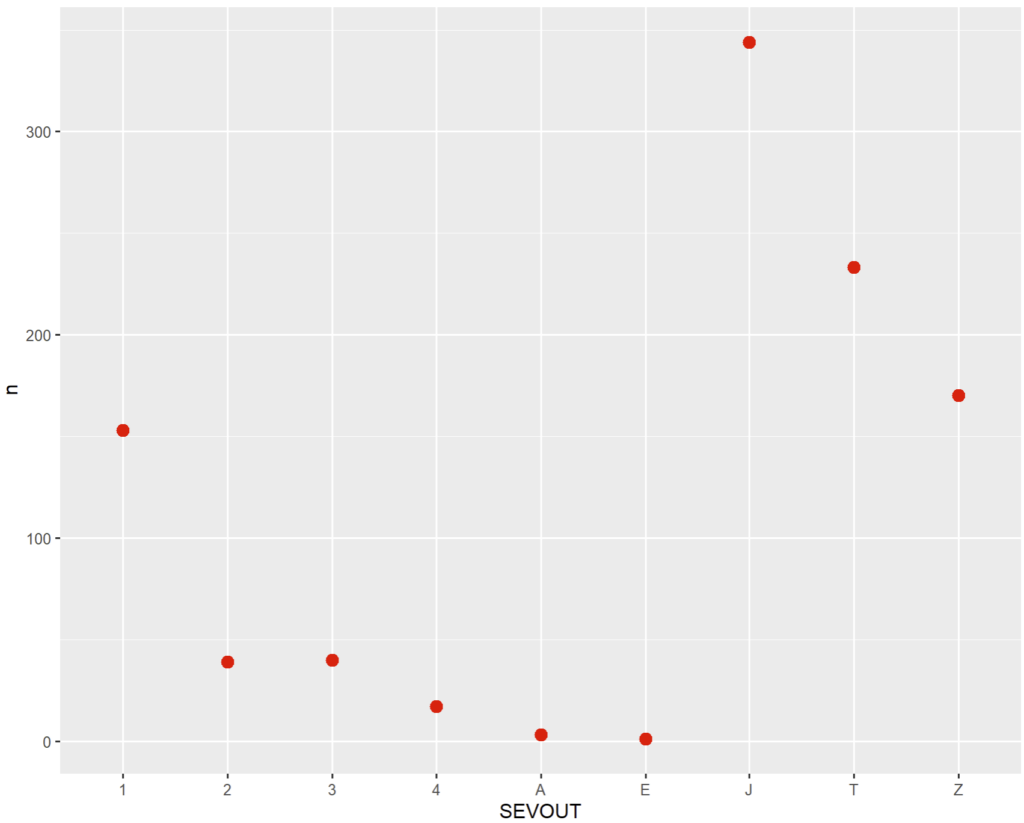
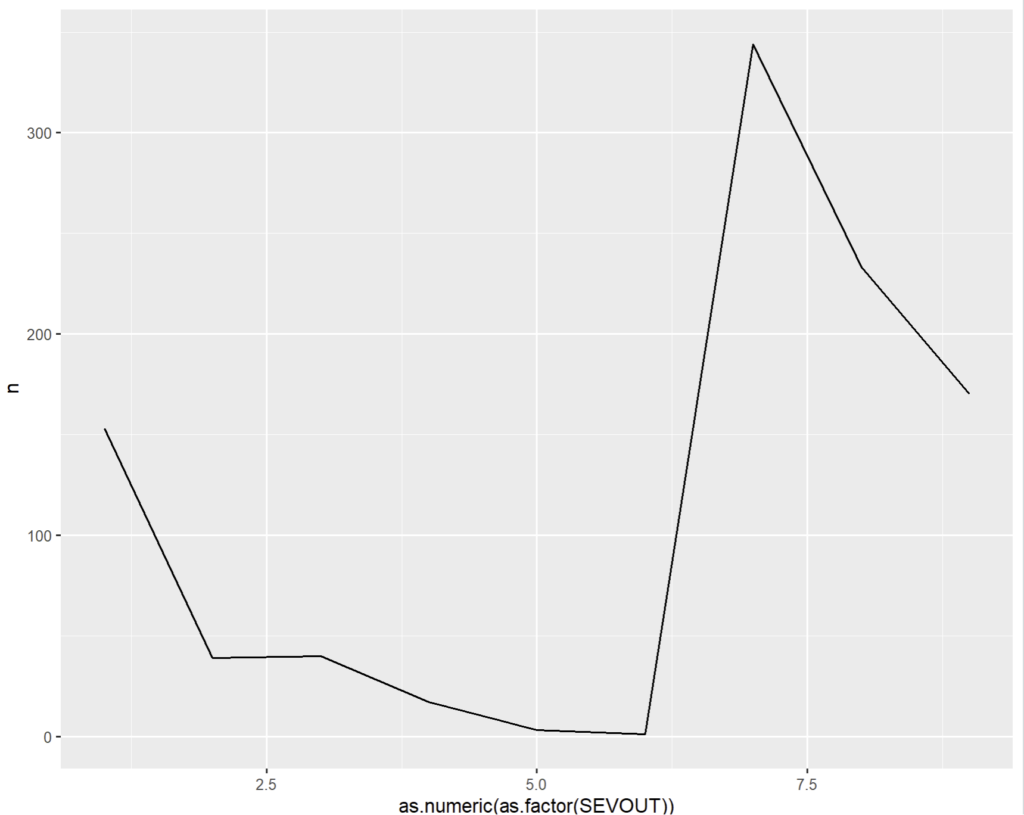
Notez qu’il est nécessaire de traduire SEVOUT qui est une variable discrète alphanumérique en une valeur numérique via as.numeric(as.factor()) pour que la courbe apparaisse car geom_path() ou geom_line() attendent exclusivement des coordonnées donc des variables continues.
Et enfin :
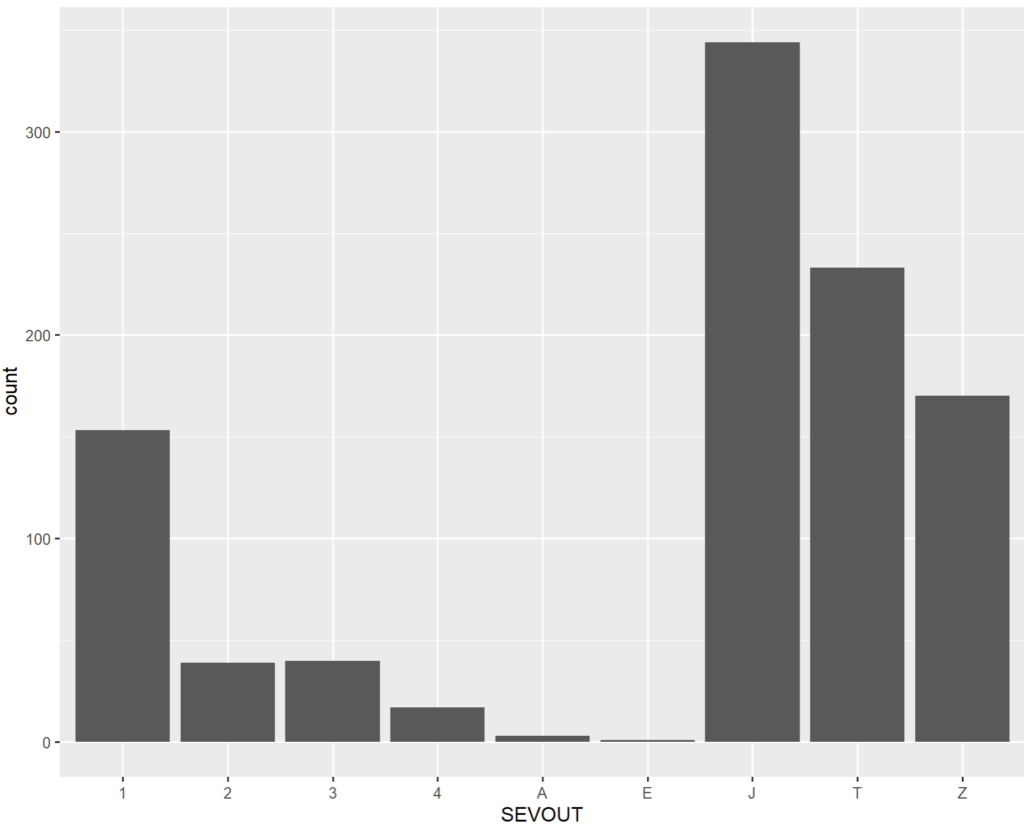
Les données sont les mêmes, cependant le graphique en barre est bien plus adapté à ces valeurs discrètes et partiellement non ordonnées.
- Le graphique en points est peu parlant car ne transmet pas l’impression de « masse » véhiculée par la surface de la barre.
- Le graphique en ligne quant à lui n’est pas pertinent car l’intervalle entre « 1 » et « 2 » voire pire entre « 4 » et « A » n’a pas de sens et donc l’approximer par une droite ne pourrait qu’apporter de la confusion ou transmettre une impression fausse à l’interlocuteur.
- Le graphique en barre aide à se représenter l’ « épaisseur » des données, le coté cumulatif de la fonction de dénombrement, en quelque sorte de faire « masse ».
Les « camemberts »
On dit graphes circulaires pour les professionnels, pie chart en anglais. Et vous vous demandez probablement pourquoi j’en parle ici…
…
…
…
…
… Et bien, imaginez vous qu’un tel graphique n’est au final qu’une vue particulière d’un histogramme. Démonstration à partir d’une variation de notre exemple déjà utilisé :
ggplot(cmd_08 %>% count(SEVOUT)) + geom_bar(aes(x="",y=n,fill = SEVOUT),stat="identity")nous donne :
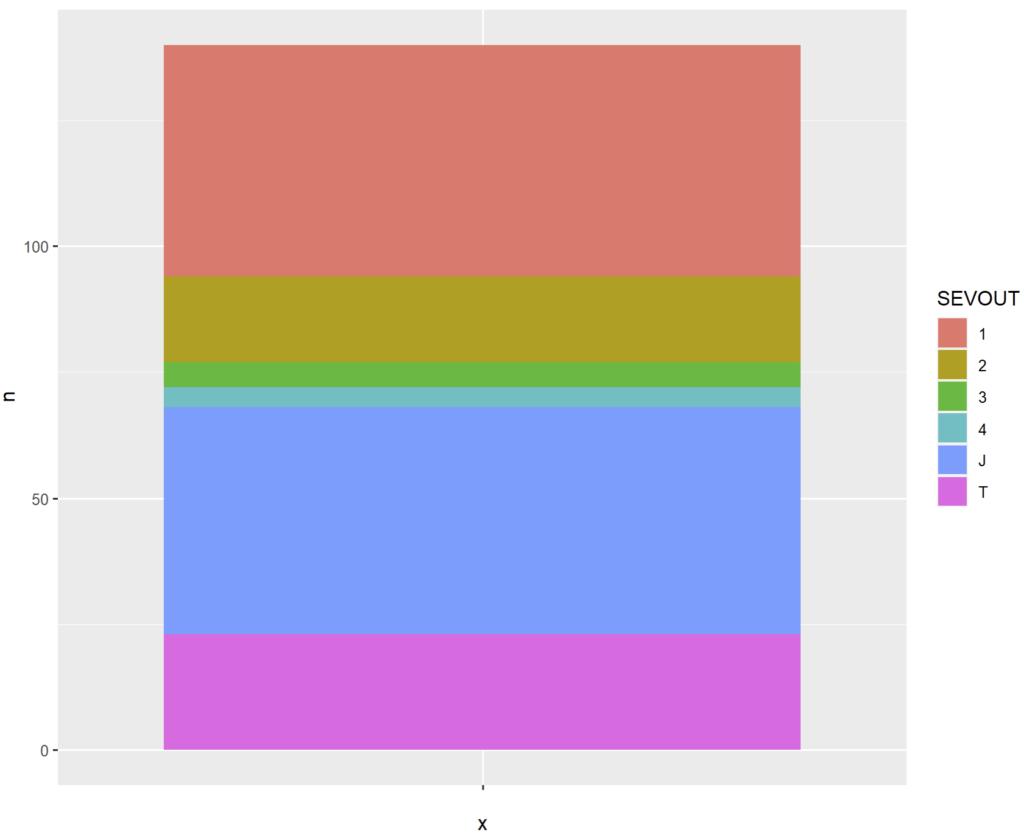
Si nous appliquons une conversion polaire via coord_polar() :
ggplot(cmd_08 %>% count(SEVOUT)) + geom_bar(aes(x="",y=n,fill = SEVOUT),stat="identity") + coord_polar("y")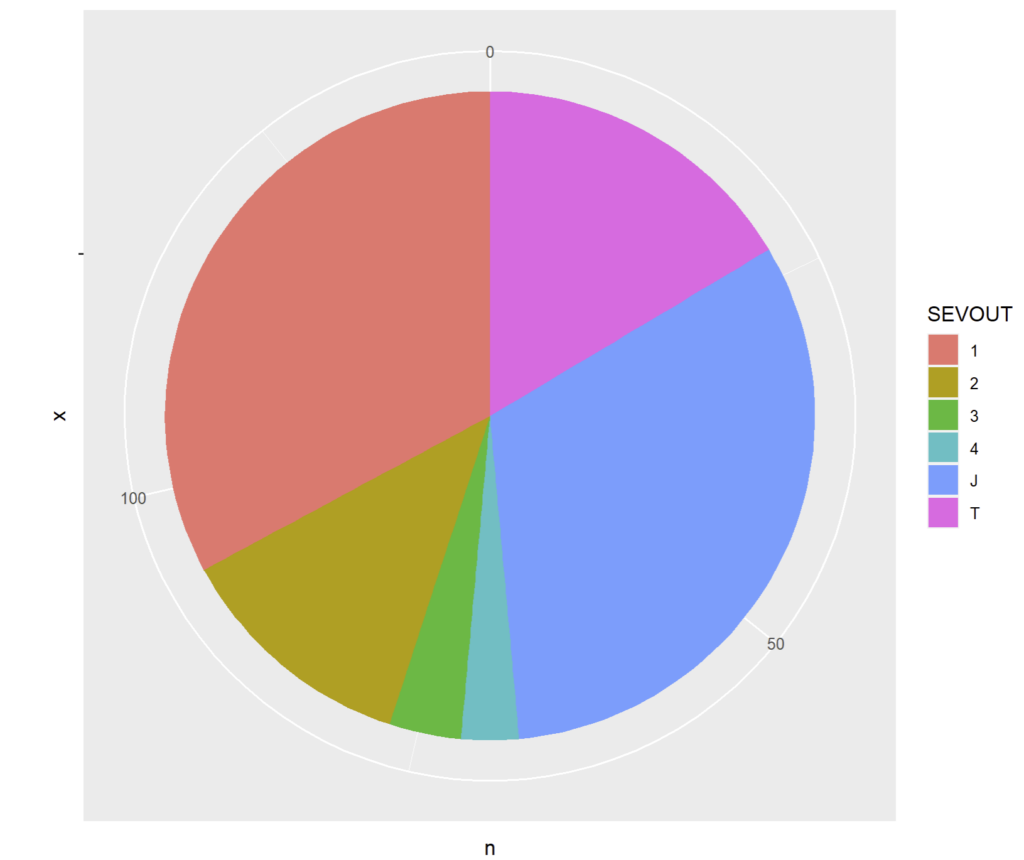
« Et voilà ! »
Il est même possible de gérer des séries créant des anneaux concentriques (donut graph en anglais) pouvant être comparées ainsi :
ggplot(cmd_08 %>% count(MOIS, SEVOUT)) + geom_bar(aes(x = MOIS,y = n,fill = SEVOUT),stat="identity",position = "fill") + coord_polar("y")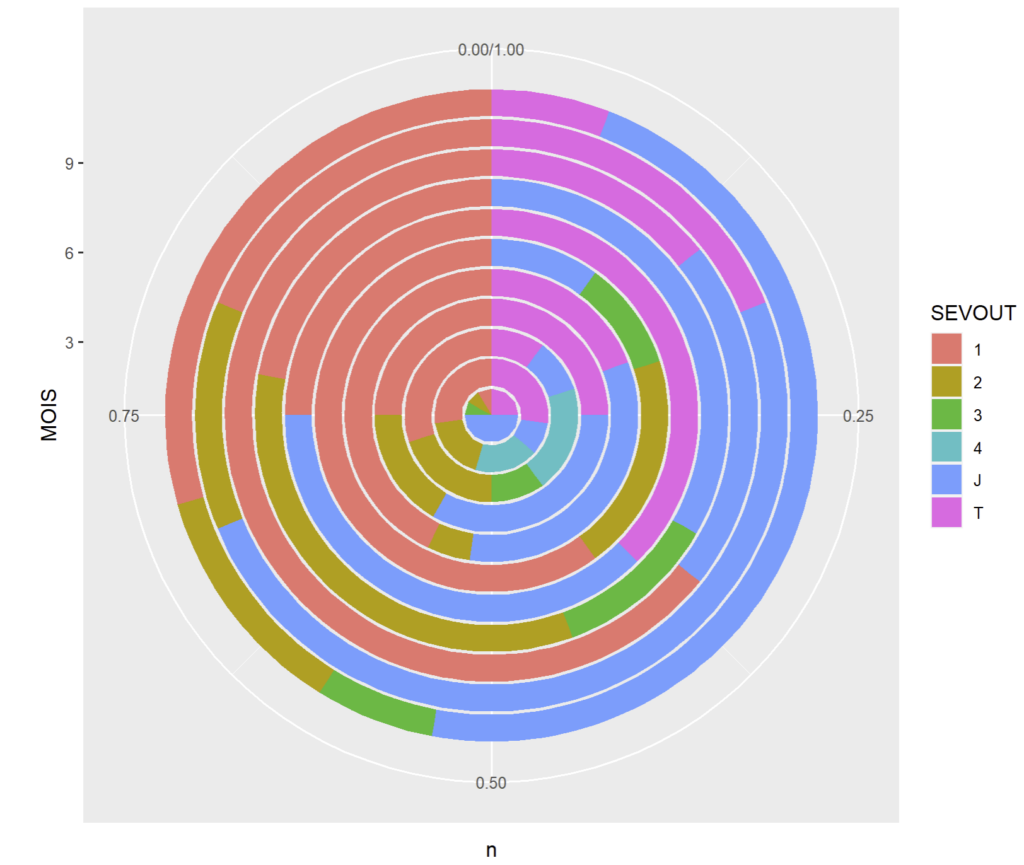
Pour ma part, je proscris les coordonnées polaires pour les histogrammes et autres données non périodiques, réservant les coordonnées polaires aux graphiques de type « radar ».
Conclusion
Nous avons fait le tour des graphiques en barre. Il faut maintenant digérer.
Mon activité professionnelle étant assez intense depuis ces derniers mois, le rythme de publication a beaucoup baissé mais une prochaine fois, nous nous pencherons sur des modes d’affichages plus exotiques. D’ici là bon entrainement !

