Les formules et l’opérateur ~ (tilde)

Aucun commentaire

Afin de préparer une série d’articles futurs, je dois vous présenter les formules (formula en anglais).

Une formule est un type d’objets R dont le type de base est language, c’est à dire un morceau de code R et la classe formula. Il est composé de 2 termes, un gauche et un droit. Le gauche étant facultatif. Et dans les faits, c’est tout. Son usage dépend du contexte et nous verrons cela plus loin.

Création d’une formule

Pour créer une formule, on utilise habituellement l’opérateur ~ (tilde) entre 2 morceaux de code R :

> a ~ b
a ~ b
R

Ce code doit être syntaxiquement correct mais n’a pas de nécessité de représenter des variables initialisées ou non :

# Code syntaxiquement correct même si aucun des noms n'est pertinent
> je_suis_une + formule(inutile) ~ et * j_en / suis (fier)
je_suis_une + formule(inutile) ~ et * j_en/suis(fier)

# Là le code est syntaxiquement incorrect, même encadré 
# par des parenthèses
> je_suis_une + formule fausse ~ et * j'en / moins suis (fier)
Error: unexpected symbol in "je_suis_une + formule fausse"
> (je_suis_une + formule fausse) ~ (et * j'en / moins suis (fier))
Error: unexpected symbol in "(je_suis_une + formule fausse"
R

Le code à gauche du ~ est facultatif mais pas le droit, on peut ainsi écrire :

# On peut créer une formule sans membre de gauche
> ~ droite
~droite

# Mais le tilde n'est pas content tant qu'on a pas saisi
# le membre de droite (là j'ai dû taper NULL mais j'aurais pû taper
# n'importe quoi
> gauche ~
+ NULL
gauche ~ NULL
R

Une fois créée, on peut manipuler une formule comme tout autre objet, par exemple l’attribuer à une variable :

> formule <- gauche ~ droite
> formule
gauche ~ droite
R

Il est aussi possible d’utiliser formula() ou as.formula() pour transformer une chaine de caractère (donc un vecteur de chaines de longueur 1 uniquement) :

> as.formula("a ~ b")
a ~ b
> formula("a ~ b")
a ~ b
R

Si on leur passe une formule, ces fonctions la retournent.

Il est aussi possible de compléter par un paramètre qui est « caché » lorsque crée par ~, un environnement, c’est à dire un ensemble de variables. Par défaut, celui-ci est celui en cours :

> as.formula(a ~ b, env = parent.frame())
R

il sert de contenant par défaut pour les variables décrites dans la formule, ici a et b.

Modification d’une formule

Je vous le mets pour référence, mais c’est très rare qu’on ait besoin de le faire.

Dans les faits, une formule se caractérise donc par 3 éléments :

  • un terme de gauche appelé « résultat »
  • un terme de droite appelé « prédicteurs »
  • un environnement

On peut les modifier grâce à des fonctions spécifiques en particulier update() en utilisant une syntaxe spéciale : le . représente le terme existant et l’intègre à sa place sinon le terme est remplacé tel quel en totalité. Si le terme de gauche est absent, un . est assumé :

> update(formule, x ~ .)
x ~ droite
> update(formule, . ~ x)
gauche ~ x
> update(formule, ~ x)
gauche ~ x
> update(formule, x ~ log(x))
x ~ log(x)
> update(formule, x ~ log(.))
x ~ log(droite)
R

et pour changer l’environnement le plus simplement possible on utilise la fonction formula() ci-dessus en lui passante la formule à modifier et le nouvel environnement dans le paramètre env=.

A quoi sert une formule ?

En gros, cette capacité d’une formule de porter du code non interprété à la création et un contenant (l’environnement) où se trouvent les valeurs décrites par la formule la destine à servir de véhicule pour ce code afin qu’il soit utilisé plus tard dans votre programme.

L’usage pour lequel les formules ont été créées est d’être passées comme paramètre principal dans un modèle. Et comme souvent en R, cet usage a été détourné (par exemple par certaines fonctions de dplyr, plot() ou ggplot2).

Ce qu’il faut retenir c’est que, en général, « ~ » veut dire « (Le résultat de) la partie gauche est en relation avec (l’interprétation de) la partie droite » (ou l’inverse).

Dans les modèles

A la base, une formule sert donc à définir l’élément de travail des modèles, c’est à dire décrire les liens existants entre des variables au sein d’un ensemble (des vecteurs séparés, un data.frame ou une matrice) en vue de le généraliser.

Pour cela, la formule nécessite de décrire les relations entre les variables. Cela se fait par une interprétation différente des symboles d’opérations arithmétiques. ATTENTION, IL NE S’AGIT PAS REELLEMENT D’ARITHMETIQUE. Ainsi si on écrit :

y ~ x
R

Cela veut dire que y est le résultat d’une « transformation » de x (y=f(x) en quelque sorte). La valeur de y est liée à (ou dépend de, choisissez votre vocable) celle de x par une relation. On peut définir des relations à plusieurs membres :

y ~ x + z
R

signifie que y dépend de x et z qui sont 2 variables quant à elles indépendantes (y=f(x,y))

y ~ x:z
R

signifie que y est le résultat de l’interaction entre les 2 variables, indépendamment de leurs valeurs respectives (y=f(g(x,y)), ça se complique)

La plupart du temps si les variables sont liées, leur valeur propre est aussi importante et cela s’écrit :

y ~ x * z
# qui est équivalent à 
y ~ x + z + x:z
R

Il est aussi possible de préciser que y dépend de toutes les valeurs présentes avec .:

y ~ .
# et on peut préciser d'en supprimer avec 
y ~ . - x
# soit toutes les valeurs sauf x
R

Il est possible de préciser le nombre  » +/-1 » pour signaler le comportement pour x = 0 :

y ~ x + 1
# signifie que pour x = 0, le modèle devra calculer
# la "valeur y d'interception" de l'axe
# Par défaut le + 1 est assumé, il n'est donc pas besoin
# de l'écrire
y ~ x
# est donc équivalent.

# si par contre on précise
y ~ x - 1
# alors on demande à ce que le modèle considère que la valeur
# de y pour x = 0 soit obligatoirement 0.

# Il est possible aussi d'écrire
y ~ 1
# qui signifie qu'on ne cherche que la valeur d'interception
# et ainsi quelle que soit la valeur de x, le modèle renvoiera
# toujours cette valeur d'interception.
R

Le symbole « ^ » suivi d’un nombre n stipule que nous voulons toutes les interractions entre variables jusqu’à l’ordre n.

y ~ (a + b + c)^3
# qui equivaut à
y ~ a + b + c + a:b + a:c + b:c + a:b:c
R

Le dernier raccourci est « %in% » qui définit une interaction avec emboitement si le modèle l’autorise :

y ~ x %in% z
# dans le cas général, c'est l'équivalent de
y ~ x:z
R

J’ai bien conscience que ce que je viens de vous présenter peut paraitre du martien mais nous allons en avoir besoin quand nous allons aborder les modèles et l’IA (zut, j’ai spoilé).

Les usages détournés de ~

Dans les graphiques

La notation de formule avec le ~ est souvent détournée pour des moments où nous voulons spécifier textuellement la relation entre 2 ou + variables. C’est le cas par exemple dans plot(), la fonction de base pour faire des graphes :

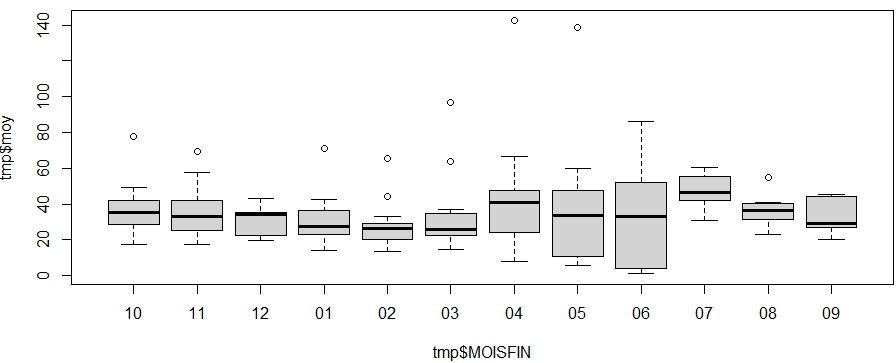
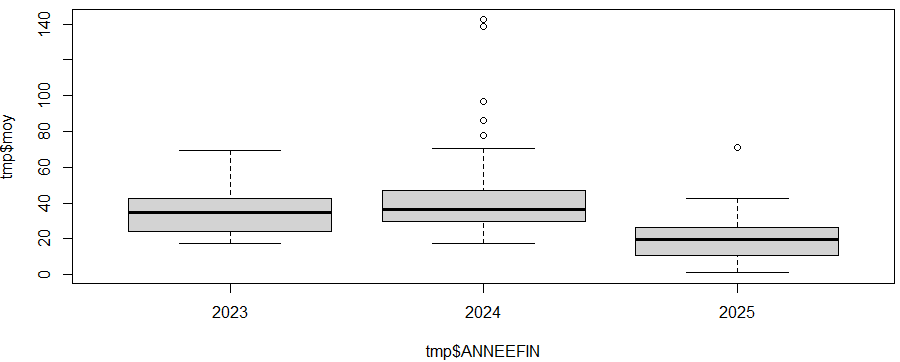
plot(tmp$moy ~ tmp$MOISFIN + tmp$ANNEEFIN)
# seul le + est disponible
R

va par exemple afficher 2 graphes (pour la petite histoire, il s’agit des moyennes de temps de groupage par mois et par an de mon DIM sur les 2 dernières années glissantes. J’ai pris le premier jeu de données que j’avais d’ouvert ! 😁) :

On peut aussi l’utiliser avec ggplot dans la fonction de création de « facet » en grille :

ggplot(groupage) + facet_grid(typeH ~ ANNEEFIN) + geom_col(aes(x=MOISFIN,y=moy,fill=moy))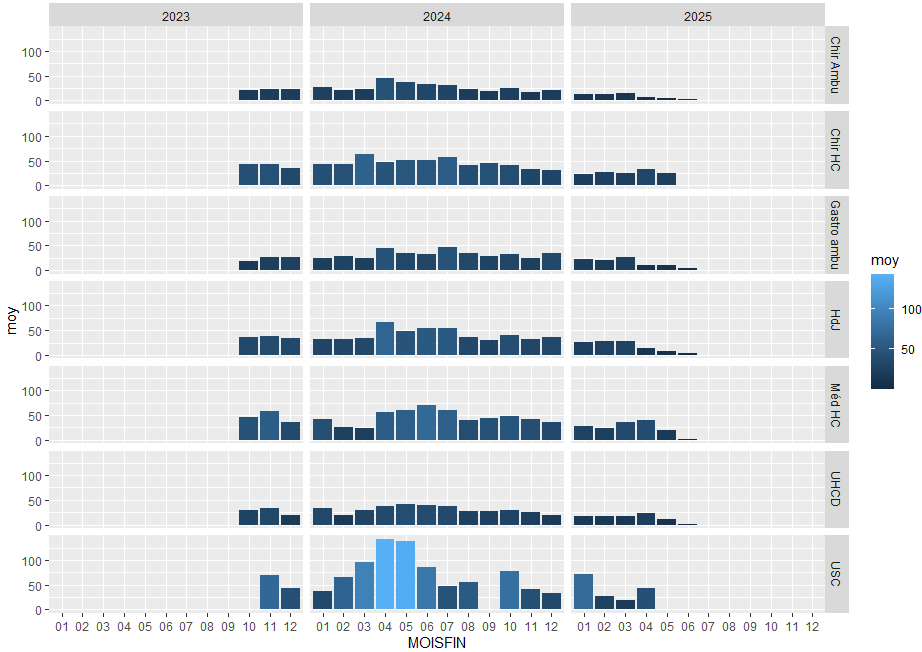
R

(Les ANNEEFIN sont en « X » et le type d’hospitalisation en « Y » puis chaque graphique par mois vient s’insérer dans la grille avec x = mois et y = nombre)

Mais parfois, ces formules sont totalement détournées de leur signification, comme par exemple dans la fonction case_when() que nous avons déjà utilisée.

case_when()

Pour rappel case_when() prend en paramètre une suite de test et leur résultat associé. Et pour les représenter, chacun d’eux est une formule respectant la forme :

case_when (test1 ~ résultat1,
           test2 ~ résultat2,
           test3 ~ résultat3,
           test4 ~ résultat4,
           .default = résultat_par_défaut)
R

où chaque testn est un morceau de code R qui sera évalué en booléen et s’il est positif retournera le résultat de l’exécution du code résultatn correspondant. Sachant que c’est le 1er positif qui gagne.

Comme vous pouvez le voir on est bien loin du formalisme des modèles. Mais cet usage astucieux du ~ est bien pratique. Il y a d’autres exemples un peu partout dans des librairies et maintenant vous comprendrez que le meilleur moyen de savoir comment saisir la pseudoformule est de lire la page d’aide de la fonction…

Conclusion

Et bien pour une fois pas grand chose. Comme je l’ai dit plus haut, une objet formule n’a d’intérêt que par ce qu’on en fait et là nous n’en avons rien fait… Il fallait cependant que je vous le présente pour que vous ne tombiez pas des nues dans 2-3 articles où vous allez voir cette notation utilisée dans sa version initiale, comme définition de relation dans des modèles.

Le prochain article va lui aussi peu parler de PMSI, et pas non plus de R (non, je ne suis pas malade et vous ne vous êtes pas trompé de site), mais plus de la grande Histoire de l’informatique et de l’intelligence (vous me voyez venir, j’imagine…) afin de servir d’introduction à une série de plusieurs articles.

Étiquettes

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *