Voici les réponses aux différentes questions de l’article « Jouons avec les tarifs »
Pour rappel vous trouverez le code d’initialisation dans le corps de l’article et le code des réponses est à rajouter à la suite.
A la fin de ce code, vous vous retrouvez avec
- GHS_N : contenant les nouveaux GHS
- GHS_R : ceux de l’année de référence
- RSA : contenant le RSA que vous voulez évaluer
Go pour les réponses !
Analyse des tarifs
Q1 : Y a-t-il de nouveaux GHS ?
Il est nécessaire de vérifier car qui dit nouveaux GHM/GHS dit nouvelle fonction groupage donc non équivalence stricte d’une année sur l’autre.
Il nous faut trouver les GHS qui se trouvent dans la table GHS_N qui ne sont pas dans la table GHS_R. Pour cela nous allons simplement utiliser anti_join().
GHS_N %>% anti_join(GHS_R, by = "GHS")Nous réalisons une jointure de sélection où seuls persisteront dans le jeu résultat les éléments de GHS_N dont le champ « GHS » n’apparait pas dans la table GHS_R
Q1bis : Corolaire, des GHS ont-il disparus ?
C’est tout simplement l’inverse du précédent :
GHS_R %>% anti_join(GHS_N, by = "GHS")Ces 2 tests permettent de vérifier qu’il n’y aura pas d’effet de non valorisation de certains séjours, perturbant en cela le case-mix valorisable.
Q2 : Des GHS présentent-ils des modifications de paramètre de calcul (bornes haute et basse) ?
Pour cette question, nous avons 2 angles d’attaque.
Par une jointure suivie d’un filtre. L’avantage principal est que cette écriture suit la démarche intellectuelle humaine (« je joins et je compare ») et nous nous retrouvons avec une table contenant les 2 jeux de données sur laquelle nous pourrions faire des calculs en suivant :
GHS_N %>% inner_join(GHS_R, by = "GHS", suffix = c(".N",".R") %>% filter(!(BH.N == BH.R & BB.N == BB.R))Mais en réalité, ce type de jointure est là-aussi réalisable par une jointure filtrante et peut s’écrire :
GHS_N %>% anti_join(GHS_R, by = c("GHS", "BH", "BB"))Dans le cas présent, nous demandons de supprimer du jeu source, les lignes dont GHS, BH et BB sont égales.
L’inconvénient est que seules les données du jeu source sont disponibles dans le résultat. Il conviendrait alors de refaire une jointure pour récupérer les 2 ensembles de paramètres.
Selon l’usage suivant de ces données, l’une ou l’autre solution est préférable.
Q3 : De combien est l’évolution moyenne des prix de base pour l’ensemble des GHS en pourcentage ? (c’est le taux qui est utilisé larga manu par les tutelles pour communiquer vers le grand public)
Le taux de base est dans GHSPRIX. Nous allons jointer de façon stricte (inner_join()) afin de ne traiter que les GHS qui existaient et continuent d’exister. Puis nous réalisons un regroupement (implicite, nous ne voulons qu’un résultat unique pour tout le jeu de données) suivi du calcul de pourcentage de variation :
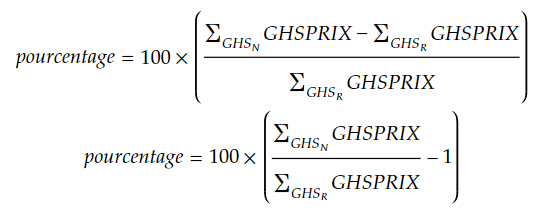
Ce qui nous donne comme code :
GHS_N %>% inner_join(GHS_R,by="GHS", suffix=c(".N", ".R")) %>%
summarise(`variation%` = 100 * (sum(GHSPRIX.N)-sum(GHSPRIX.R))/sum(GHSPRIX.R))
# ou
GHS_N %>% inner_join(GHS_R,by="GHS", suffix=c(".N", ".R")) %>%
summarise(`variation%` = 100 * (sum(GHSPRIX.N)/sum(GHSPRIX.R)-1))(Même si sum(GHSPRIX.R) semble être calculé deux fois dans le 1er code, le temps d’exécution des 2 versions est superposable)
Q4 : De combien le prix de base (GHSPRIX) a-t-il évolué pour chaque GHS en valeur absolue et en pourcentage ?
Dans la question précédente, nous avons calculé la variation pour l’ensemble du jeu de données. Ici nous voulons la faire par GHS. Il nous faut donc constituer un jeu modifié. Il nous faudra :
GHS, CMD, CATGHM et la variation. Nous nommons ce résultat intermédiaire afin de pouvoir y faire référence dans les visualisations sans devoir recalculer.
comparaison_GHS <- GHS_N %>% inner_join(GHS_R,by="GHS", suffix=c(".N", ".R")) %>%
mutate(CMD = substr(GHM.N, 1,2),
CATGHM = substr(GHM.N,3,3),
`variation%` = 100 * ((GHSPRIX.N/GHSPRIX.R)-1)) %>%
select(GHS, CMD, CATGHM, `variation%`)Cela nous donne une table comme ceci sur laquelle nous allons pouvoir travailler notre visualisation.
# A tibble: 3,698 × 4
GHS CMD CATGHM `variation%`
<dbl> <chr> <chr> <dbl>
1 22 01 C 3.05
2 23 01 C 3.05
3 24 01 C 3.05
4 25 01 C 3.05
5 26 01 C 3.05
6 27 01 C 3.05
7 28 01 C 3.05
8 29 01 C 3.05
9 30 01 C 3.05
10 31 01 C 3.05
# ℹ 3,688 more rows
# ℹ Use `print(n = ...)` to see more rowsLe taux théorique d’évolution est donc égal à la moyenne de « variation% ». Pour l’avoir, il suffit de faire par exemple :
> mean(comparaison_GHS$`variation%`)
4.5Voilà : +4,53% d’évolution faciale moyenne des tarifs. Et de la même manière vous pouvez trouver les extrêmes en utilisant min() et max() : Minimum = +3,05% , Maximum = +11,86%
Représenter graphiquement la fréquence du pourcentage d’évolution en fonction de la CMD
Il y a plusieurs façon de réaliser cette visualisation. Le problème particulier dans cet exercice est la quantité de données présentes qui se superposent et le nombre de CMD (28) qui encombre la vue. La bonne solution de visualisation à mes yeux et d’utiliser du « facetage » :
ggplot(comparaison_GHS +<br> facet_wrap(vars(CMD),scales="free_y")+
geom_histogram(aes(x=`variation%`),binwidth = 1)Ce qui nous donne un affichage de ce type :
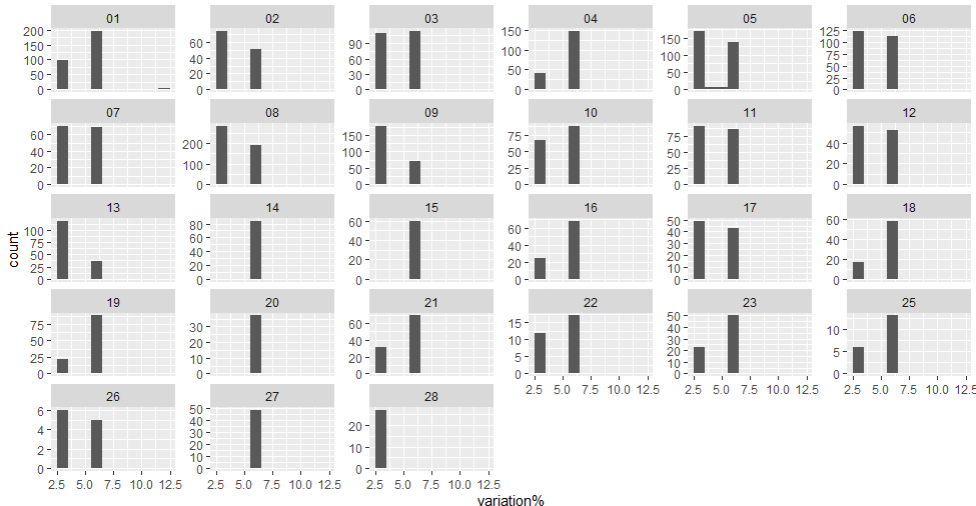
Cela nous permet de voir que l’évolution des tarifs est surtout portée par 2 tranches, une aux alentours de 3% et une autre vers 5,8% (avec quelques exceptions par exemple en CMD01 où existent, à la marge, des +11%) et que la répartition entre ces 2 taux varie en fonction de la composition en GHM des CMD
Puis en fonction du type de GHM
Le principe est le même :
ggplot(comparaison_GHS +
facet_wrap(vars(CMD),scales="free_y")+
geom_histogram(aes(x=`variation%`),binwidth = 1)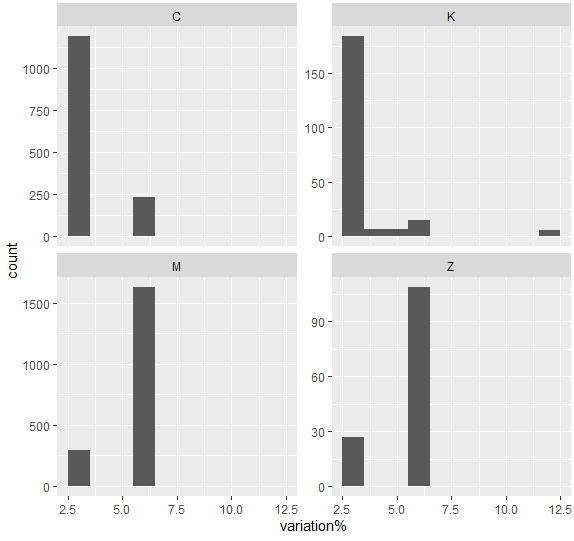
Ce qui était « dissous » dans le tableau des CMD devient plus clair : Les séjours mieux revalorisés sont des séjours de médecine (non chirurgicaux et non techniques).
Je vous laisse continuer à morceler d’avantage les tarifs selon d’autres caractéristiques des GHM, c’est assez édifiant.1
Valorisation
Maintenant que nous avons regardé le fichier indépendamment de l’activité de l’établissement. Il faut bien se concentrer sur celle-ci. En effet, la revalorisation de l’UNV à 11% n’a d’intérêt… que si on a une UNV…
Pour cela nous avons chargé un RSA dans lequel nous avons les 2 champs capitaux : le GHS attribué par la Fonction Groupage et la durée de séjour « DS ».
Q1 : Valorisez votre activité réelle
Dans le code donné en début de l’article précédent, la fonction valorise_ghs.df() permet de valoriser en une passe tout le jeu de données transmis en paramètre. Le paramètre ghss= doit contenir la table des GHS a utiliser pour la valorisation, annee_col= fixe la colonne dans laquelle se trouve l’année de valorisation, tandis que out_col= contient la colonne qui recevra la valorisation.
Dans le RSA présent, il manque des colonnes avec les années pour pouvoir traiter correctement les données et nous fixons à valoREF et valoNOUV les nouvelles colonnes qui contiendront les valorisations respectivement de référence et des nouveaux tarifs.
RSA_valorise <- RSA %>%
mutate(ANNEE_N = as.character(ANNEE_N), ANNEE_R = as.character(ANNEE_R)) %>%
valorise.ghs_df(ghss = GHS_R, out_col = "valoREF", annee_col = "ANNEE_R") %>%
valorise.ghs_df(ghss = GHS_N, out_col = "valoNOUV", annee_col = "ANNEE_N") %>%
mutate(gain = valoNOUV - valoREF)Nous nous retrouvons avec 1 ligne par séjour
Q2 : Et votre case-mix
Un case-mix consiste à transformer un ensemble de séjours en une description synthétique moyenne : GHS / DMS / nombre de séjours
Cela se fait par un regroupement (group_by() %>% summarise() ) :
RSA %>% group_by(GHS,GHM = GHMOUT) %>% summarise(n=n(),DMS=mean(DS))Ensuite nous pouvons valoriser ce case-mix :
casemix_valorise <- RSA %>% group_by(GHS,GHM = GHMOUT) %>% summarise(n=n(),DMS=mean(DS)) %>%
mutate(ANNEE_N = as.character(ANNEE_N), ANNEE_R = as.character(ANNEE_R)) %>%
valorise.ghs_df(ghss = GHS_R, out_col = "valoREF", ds_col="DMS", annee_col = "ANNEE_R") %>%
valorise.ghs_df(ghss = GHS_N, out_col = "valoNOUV", ds_col="DMS", annee_col = "ANNEE_N") %>%
mutate(gain = n*(valoNOUV - valoREF),`%`= 100*gain/(n*valoREF))Nous nous retrouvons donc avec 1 ligne par GHS.
La valorisation d’activité se fait ensuite par une sommation de toutes les lignes, qu’il s’agisse du RSA directement ou du case mix. Le code est similaire :
(...) %>% summarise(valoREF = sum(valoREF, na.rm = TRUE),
valoNOUV = sum(valoNOUV, na.rm = TRUE),
gain = sum(gain,na.rm = TRUE),
`%` = 100 * gain / valoREF)Q3 : Qu’est-ce qui explique cette différence ?
Sur un établissement fictif créé pour l’occasion, voici le type de données renvoyées en cas de valorisation réelle :
# A tibble: 1 × 4
valoREF valoNOUV gain `%`
<dbl> <dbl> <dbl> <dbl>
1 21095827. 21971338. 875511. 4.15Alors que la méthode par le case-mix donne :
# A tibble: 1 × 4
valoREF valoNOUV gain `%`
<dbl> <dbl> <dbl> <dbl>
1 20840580. 21702024. 861444. 4.13Donc oui, en effet il y a une différence. Mais elle n’est pas « énorme » (0,02%) permettant de valider l’usage du case-mix pour une évaluation approximative de ce genre plutôt que le recours systématique au RSA.
Cependant, il faut bien comprendre que seul le RSA donnera un chiffre basé sur du réel.
La différence entre ces 2 ensembles de valeurs provient simplement de l’amortissement des séjours extrêmes (en particulier hauts) par le calcul de la DMS lors de la constitution du case-mix et son usage dans la valorisation (écrêtant les EXH et les rares EXB).
Q4 : Quel est votre pourcentage d’évolution réel ?
Vous avez la réponse en bout de ligne des résultats précédents dans la colonne « % ». A comparer donc avec le taux annoncé dans la presse et que nous avons calculé plus haut à 4,53%… Eeeeet pour notre malheureux établissement, il y a déjà 40 points de perdus avant déduction des transferts de charge (mais cela n’est pas/plus du périmètre du DIM mais de la DAF) définis parallèlement à l’arrêté.
Conclusion
Voilà, j’espère que vous avez tout trouvé. Si vous avez des questions n’hésitez pas.
- En 2024, en étudiant les GHM par catégorie de GHM, CMD et niveaux de sévérité. On peut s’apercevoir que ne sont pas dans les mieux revalorisés : la quasi totalité des séjours de chirurgie, la plupart des séances et les GHM sans sévérité au profit de séjours médicaux à sévérité, quelques niches (Brûlures, néonatologie, UNV) et l’obstétrique. Je vous laisse le caractériser numériquement et graphiquement.
↩︎
