Sans IA « boîte noire », sans mathématiques avancées (mais une intro discrète au Machine Learning)
Lorsqu’un patient est admis, le DIM dispose déjà de plusieurs informations : âge, mode d’entrée, type de séjour, orientation prévue…
Lors de sa sortie, le codage reste à faire mais parfois on nous demande déjà une valorisation. Ce qui, selon l’organisation du service et la qualité du dossier, est souvent impossible.
Mais sans chercher à prédire le codage final ni à remplacer l’analyse médicale, peut-on estimer un ordre de grandeur de la valorisation attendue, uniquement à partir de ces éléments initiaux ?
L’objectif n’est pas la perfection, mais une aide à l’anticipation médico-économique, explicable et reproductible.
Le cadre de travail
Les librairies
Nous aurons besoin des grands classiques pour rendre R agréable mais rien d’exceptionnel :
library(dplyr)
library(ggplot2)
library(tibble) # uniquement pour créer à la main de façon visuelle un jeu de données grâce à la fonction tribble()
library(readr) # pour charger le CSV visualValoSejours si vous utilisez cette source.Les autres fonctions sont déjà dans Rbase.
Les données
Pour les différents exemples au fur et à mesure de l’article, on va supposer disposer d’un jeu de données de séjours MCO d’où nous allons supprimer la plupart des éléments discriminants pour le PMSI. Nous garderons :
- valorisation : valorisation observée du séjour (GHS ou équivalent, vous choisissez)
- type_sejour : HC / HTP
- ds : durée de séjour observée (en jours)
Un tel jeu de données pourrait se créer, par exemple à partir du fichier visualValoSejours (si vous avez lu d’autres articles du site, vous devez savoir le charger, sinon je vous mets une version ci-dessous) :
visualValo <- read_delim("<chemin vers votre fichier>",
delim = ";", escape_double = FALSE, locale = locale(),
trim_ws = TRUE) %>%
mutate(DATE_ENT=as.Date(DATE_ENT,format="%d%m%Y"),
DATE_SOR=as.Date(DATE_SOR,format="%d%m%Y"))Puis on ne garde que ce qu’on va utiliser. (on pourrait bien sûr chainer les 2 traitements)
sejours <- visualValo %>%
mutate(ds = as.numeric(DATE_SOR - DATE_ENT),
type_sejour = ifelse(ds == 0, "HTP", "HC"),
valorisation = MNT_GHS) %>%
# On ne garde que le principal. (Techniquement même NO_ADMIN est inutile mais
# si on voulait retrouver un dossier en particulier, c'est nécessaire)
select(NO_ADMIN, valorisation,type_sejour, ds)Ensuite, je vous laisse créer de la façon que vous désirez une autre table contenant les entrées à analyser. Par exemple :
sejours_du_jour <- tribble(
~NO_ADMIN, ~ds, ~type_sejour,
1, 0, "HTP",
(...)
100, 10, "HC")Ou en l’extrayant de votre DPI (par exemple tous les séjours sortis sur le dernier mois).
Point de départ : si je ne sais rien du séjour
Avant d’introduire la moindre information, posons la question la plus simple possible :
« Si je ne sais absolument rien d’un séjour, que puis-je dire de sa valorisation ?«
La seule réponse raisonnable est : la moyenne des valorisations des séjours observés. C’est ce qu’on appelle communément le Poids/Prix Moyen du Cas Traité (PMCT).
Nous pouvons le calculer simplement (bien sûr ce chiffre dépend du fichier source donc de l’activité étudiée) :
> mean(sejours$valorisation)
1998.307mais nous pouvons aussi l’écrire comme une modélisation :
m0 <- lm(valorisation ~ 1, data = sejours)Ce modèle signifie :
« Tous les séjours se valent, indépendamment de tout paramètre. »
Vous devez avoir reconnu en premier paramètre une formule, déjà expliquée dans l’article idoine tandis que le paramètre data= reçoit les données dont nous connaissons déjà la valorisation et qui vont servir à « entrainer » le modèle.
Vous pouvez visualiser le résultat avec un ggplot :
sejours %>%
mutate(pred = predict(m0)) %>%
ggplot(aes(x = valorisation, y = pred)) +
geom_point(alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, linetype = "dashed") +
labs(
title = "Modèle naïf : tous les séjours valent la moyenne",
x = "Valorisation réelle",
y = "Valorisation estimée"
)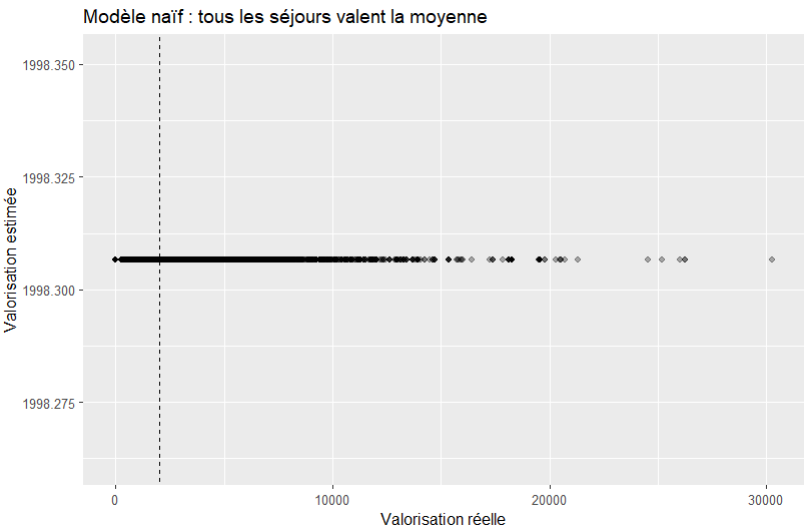
La fonction predict(), comme son nom l’indique va prédire la valorisation selon nos paramètres tirés du modèle précédent m0 (soit aucun pour le moment).
Ce modèle est évidemment très imparfait vu que tous les séjours ont la même valorisation, mais il constitue notre point zéro. il faut bien avouer que pour le moment, ce n’est pas très « sexy »…
Introduire une information évidente : HC vs HTP
Un DIM sait que tous les séjours ne se valent pas.
La première distinction naturelle est le type de séjour.
Nous pouvons écrire un nouveau modèle :
m1 <- lm(valorisation ~ type_sejour, data = sejours)Ce modèle se lit :
« la valorisation dépend du type de séjour. (Ici, hospitalisation complète ou de jour/ambulatoire) »
Il crée 2 catégories HC et HTP et va calculer un PMCT séparé pour chacune.
sejours %>%
mutate(pred = predict(m1)) %>%
ggplot(aes(x = valorisation, y = pred, color = type_sejour)) +
geom_point(alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, linetype = "dashed") +
labs(
title = "Prise en compte du type de séjour",
x = "Valorisation réelle",
y = "Valorisation estimée"
)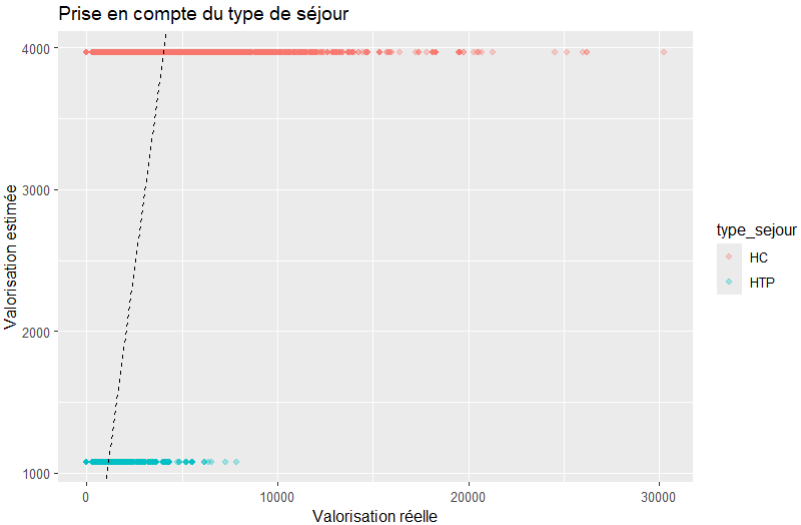
Ce modèle ne « comprend » rien au médical.
Il constate simplement que certains groupes de séjours ont des valorisations moyennes différentes et le restitue lors de la prediction.
Là encore, on est bien loin de la ligne de référence mais il y a un peu de « sens ».
On pourrait aussi séparer en HC_chirurgie, HC_médecine, HTP_chirurgie, HTP_médecine, ou tout autre type de votre choix selon les données que vous pouvez récupérer.
La durée de séjour : un bon sens… piégeux
Intuitivement, quand on regarde de loin le PMSI, on pense constater que :
« plus un séjour dure, plus il mobilise de ressources. »
Essayons de traduire ce bon sens tel quel toujours avec notre formule :
m2 <- lm(valorisation ~ ds, data = sejours)Ce qui signifie :
« La valorisation varie en fonction de la durée de séjour. »
Mais plus exactement car c’est un modèle linéaire, il suppose implicitement que :
Chaque jour supplémentaire “vaut” la même chose,
qu’on passe de 1 à 2 jours ou de 20 à 21 jours.
Comme précédemment on peut le visualiser :
sejours %>%
mutate(pred = predict(m2)) %>%
ggplot(aes(x = valorisation, y = pred, color = type_sejour)) +
geom_point(alpha = 0.3) +
geom_abline(slope = 1, intercept = 0, linetype = "dashed") +
labs(
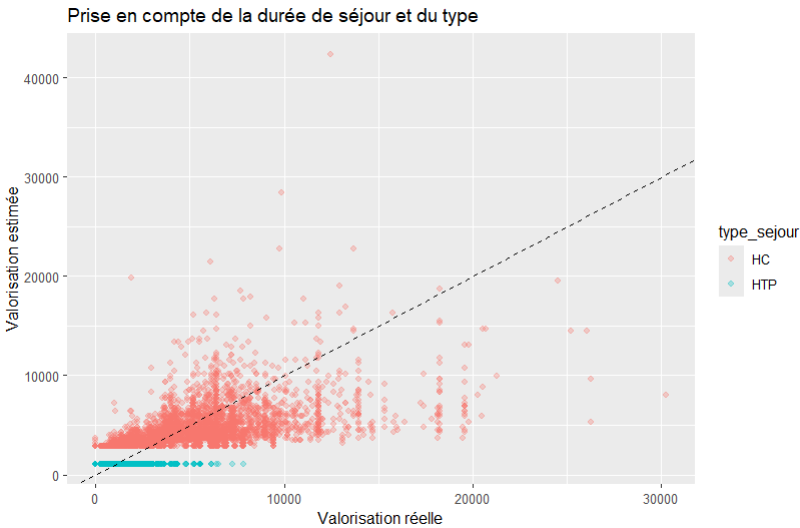
title = "Prise en compte de la durée de séjour",
x = "Valorisation réelle",
y = "Valorisation estimée"
)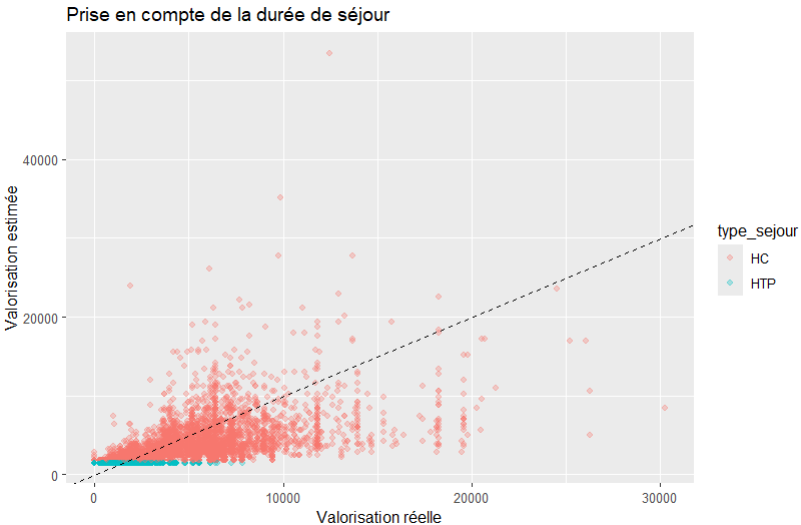
Mais aussi en fonction de la DS :
sejours %>%
mutate(pred = predict(m2)) %>%
ggplot(aes(x = ds)) +
geom_point(aes(y=valorisation),alpha = 0.3) +
geom_point(aes(y=pred),alpha = 0.3, color = "red") +
labs(
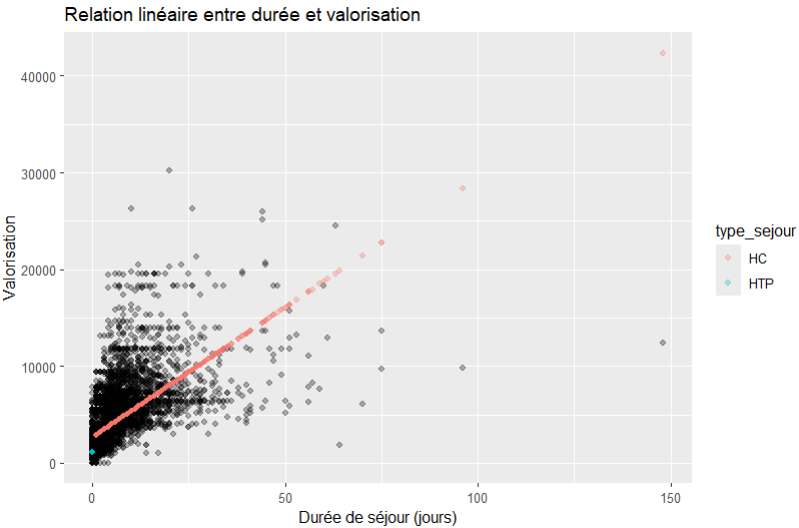
title = "Relation linéaire entre durée et valorisation",
x = "Durée de séjour (jours)",
y = "Valorisation"
)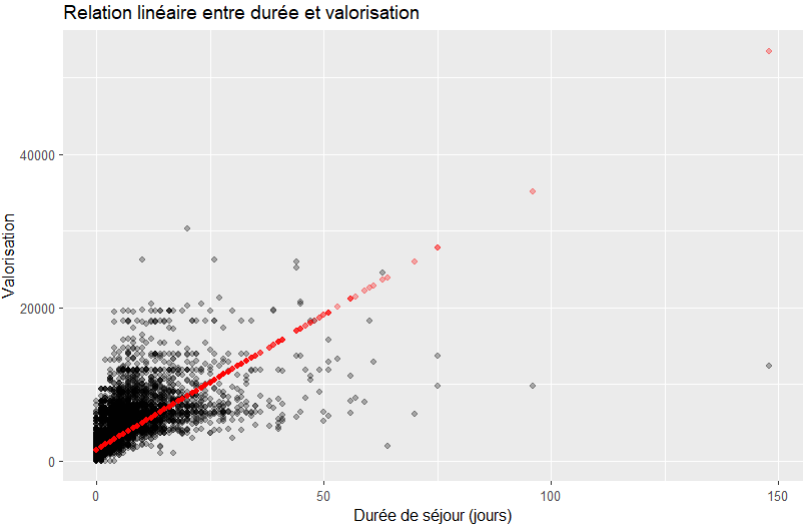
Au moins on commence à voir poindre un début de proportionnalité.
Les DIM reconnaissent immédiatement le problème que ce soit sur les séjours courts ou longs, la dispersion est parfois énorme. Et le problème que les séjours ambulatoires sont très souvent beaucoup plus valorisés rapportés à la DS, ce que ce modèle simpliste ne sais traduire.
Cependant, cela ne disqualifie pas pour autant l’utilisation d’un tel modèle, c’est juste qu’il faut le prendre avec ses inconvénients et connaitre ses limites.
Combiner type de séjour et durée
m3 <- lm(valorisation ~ type_sejour + ds, data = sejours)Ce modèle dit :
« À type de séjour identique, la durée agit comme un curseur de valorisation. »
Bien sûr, vous pouvez visualiser le résultat avec le code ci-dessus adapté.
Le modèle progresse, mais une limite majeure subsiste.
Un point clé : la durée n’a pas le même poids tout au long du séjour
Sans employer de termes mathématiques, on peut formuler le problème ainsi :
Les premiers jours comptent plus que les suivants.
Plutôt que de raisonner jour par jour, adoptons une logique par phases de séjour, beaucoup plus proche du raisonnement clinique.
Raisonner par paliers de durée
On découpe la durée en classes simples (un peu arbitraires) :
- 0–2 jours
- 3–5 jours
- 6–10 jours
- 10-30 jours
- plus de 30 jours
Ca n’est pas parfait, car en médecins DIM que nous sommes, nous savons que c’est le couple GHM/DS qui définit les classes en fonction des CMA. Mais justement nous ne cherchons pas la perfection mais un moyen d’estimer sans avoir fait le codage (donc sans le GHM).
Nous allons donc rajouter une variable à notre jeu de données, la classe de DS ds_classe=
sejours <- sejours %>%
mutate(
ds_classe = cut(
ds,
breaks = c(0, 2, 5, 10, 30,Inf),
labels = c("0-2", "3-5", "6-10", "10-30", "30-"),
include_lowest = TRUE,
right=FALSE
)
)Puis nous pouvons créer encore un nouveau modèle :
m4 <- lm(valorisation ~ ds_classe + type_sejour, data = sejours)ou bien encore un qui prend en compte classe de DS et la DS elle-même :
m4_bis <- lm(valorisation ~ ds_classe + ds + type_sejour, data = sejours)Et nous pouvons les visualiser en adaptant notre code :
sejours %>%
mutate(pred = predict(m4), pred_bis=predict(m4_bis)) %>%
ggplot(aes(x = ds)) +
geom_point(aes(y=valorisation),alpha = 0.3) +
geom_point(aes(y=pred),alpha = 0.3, color = "red") +
geom_point(aes(y=pred_bis),alpha = 0.3, color = "blue") +
labs(
title = "Relation linéaire entre durée et valorisation",
x = "Durée de séjour (jours)",
y = "Valorisation"
)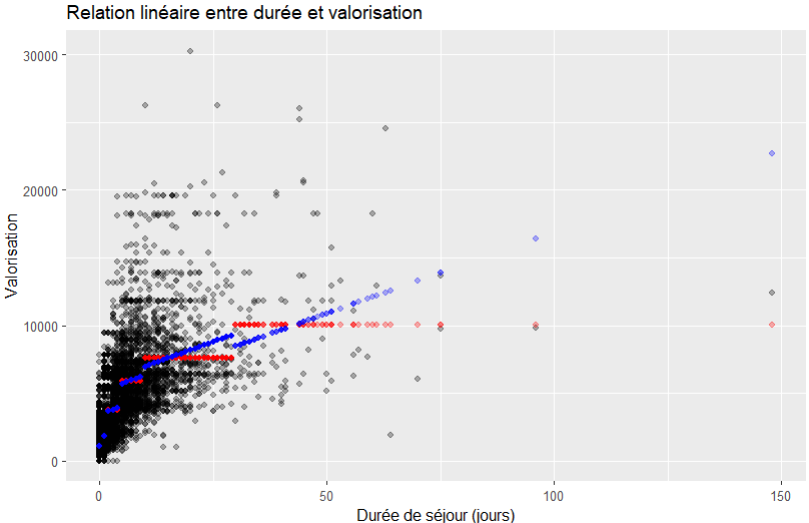
en rouge le modèle m4,
en bleu le modèle m4_bis)
Le modèle m4 n’est pas plus complexe mais semble plus réaliste et le modèle m4_bis l’affine encore un peu plus au sein de chaque classe définie par type_sejour.
En ensuite ? Choisir le modèle
Une fois tous les modèles pouvant sortir de l’esprit malade d’un DIM prêts, il faut choisir celui à utiliser. Pour cela il existe plusieurs critères mais nous allons ici utiliser le plus simple à comprendre.
Nous allos calculer l’erreur moyenne, c’est à dire :
En moyenne, de combien d’euros le modèle considéré se trompe-t’il ?
Nous pouvons écrire une fonction qui calcule l’erreur moyenne et je rajoute aussi la définition d »un autre indicateur, l’erreur cumulée :
# "donnees = sejours" dans la définition de la fonction
# n'est pas réellement nécessaire de même que le paramètre
# data= dans l'appel à predict(). Mais je trouve ça plus propre.
erreur_moyenne <- function(modele,donnees = sejours) {
mean(abs(donnees$valorisation - predict(modele, newdata = donnees)))
}
# = moyenne de la valeur absolue de la différence entre la prediction
# et la valeur réelle
erreur_cumulee <-function(modele,donnees = sejours) {
sum(donnees$valorisation) - sum(predict(modele, newdata = donnees))
}
# = différence brute entre la valorisation totale réelle et la somme des
# valeurs prédites sur l'ensemble des donnéesEt on en fait un tableau de résultat :
options(scipen = 10) # juste pour ne pas avoir une représentation
# en notation scientifique des très petits
# et très grands nombres
> data.frame(
modele = c("Moyenne seule",
"Type séjour",
"Durée linéaire",
"Durée par classes",
"Durée par classes et linéaire"),
erreur_moyenne = c(
erreur_moyenne(m0),
erreur_moyenne(m1),
erreur_moyenne(m3),
erreur_moyenne(m4),
erreur_moyenne(m4_bis)
),
erreur_cumulee = c(
erreur_cumulee(m0),
erreur_cumulee(m1),
erreur_cumulee(m3),
erreur_cumulee(m4),
erreur_cumulee(m4_bis)
)
)
modele erreur_moyenne erreur_cumulee
1 Moyenne seule 1580.1106 -0.0000023245811
2 Type séjour 1158.8528 0.0000104457140
3 Durée linéaire 999.9786 0.0000051781535
4 Durée par classes 941.7695 0.0000009685755
5 Durée par classes et linéaire 934.6848 0.0000007003546Ce tableau se lit ainsi :
En utilisant le modèle « Moyenne seule », l’erreur de valorisation moyenne est de 1580€ (pour rappelons-le un séjour moyen à 1998 € ce qui semble être énorme, une erreur moyenne de 80% !).
En utilisant un modèle plus métier, on améliore l’erreur de valorisation moyenne (qui passe à 46%).
Cependant l’erreur est ridicule en cumulé dans tous les cas.
Le message est clair :
Sans sophistication mathématique, une meilleure représentation métier améliore l’estimation d’un séjour isolé (sans pour autant être parfait loin s’en faut !).
Et corolaire en étudiant l’erreur cumulée
A un niveau « macro », le PMCT (ou les autres modèles) reste une pas trop mauvaise estimation de l’activité sans prise de tête même si on gagne un peu en précision avec les modèles métiers.
En quoi est-ce déjà une forme d’IA ?
Le modèle ne raisonne pas comme un médecin DIM qui donnerait un chiffre exact après application des règles de codage, groupage et valorisation (mais qui prendra le temps nécessaire pour le faire).
Il apprend à partir des séjours passés comment combiner des informations simples et facilement disponibles pour produire une estimation. Le médecin DIM infuse simplement un peu de sens métier dans le choix des paramètres (ici le type de séjour, puis la DS, puis des catégories de DS) pour affiner le résultat.
Les algorithmes de Machine Learning plus avancés font exactement la même chose, avec plus de variables et moins de contraintes sur la forme des relations. Et pour certains, ils apprennent d’eux-même les paramètres pertinents ou non.
Ici, nous avons volontairement limité la complexité, privilégié l’explicabilité, conservé un raisonnement lisible pour un DIM. C’est pour cela que j’ai utilisé un modèle de régression linéaire qui au final est plus un outil statistique que de machine learning.
Et on peut dire qu’on s’en tire pas si mal pour au final avec seulement 1 ou 2 lignes de code R…
Ce que fait — et ne fait pas — ce type de modèle
Car c’est tout le noeud du problème lorsqu’on utilise des outils de modélisation statistique, de machine learning ou d’IA en général ; il faut connaitre et maitriser les périmètres d’usage de l’outil.
Dans nos exemples, les résultats de ces modèles peuvent :
- Aider à l’anticipation médico-économique (pour donner des réponses précoces à la direction éventuellement en autonomie)
- Identifier précocement des séjours atypiques (pour adapter le traitement par les TIMs en fonction de leur niveau d’expertise)
- Etre utilisés comme support précoce à la discussion avec les équipes soignantes (dialogue de gestion, mais attention au risque de pinaillage vu que ce ne sont que des estimations…)
Par contre, sachez ne pas vous emballer car comme toute modélisation, tomber strictement sur le bon résultat relève du hasard (minoration de l’erreur moyenne mais qui n’arrivera pas à 0 et que là nous n’avons pas descendu en dessous de 46%…). Ainsi, vous n’atteindrez jamais :
- la prédiction exacte du codage final (qui ne peut être garantie qu’en appliquant les règles normales de production)
- la substitution au raisonnement médical (il faudra toujours coder les séjours)
- la vérité individuelle sur un patient donné (car nous parlons de regroupements de patients, pas des GHM mais une autre classification personnalisée au final)
Aller plus loin ?
On pourrait toujours tenter d’améliorer ce modèle par exemple en rajoutant des éléments discriminants. On peut imaginer :
- la 1ère UF
- le passage ou non par les urgences
- le passage en USC
- l’âge
- …
Tout peut être envisagé. Cependant, il faut toujours penser à une chose : plus on affine, plus on diminue la taille des échantillons et donc plus on va être sensible à des biais ou des valorisations atypiques. La connaissance et la maitrise des caractéristiques de population et de ses données sont la clé d’un modèle et d’une simulation réussie !
Un autre écueil est intrinsèque au modèle utilisé ici, la régression linéaire : Ce modèle considère que toute variable numérique suit une droite (que son incidence sur la valorisation est du type yn=an.xn+bn), ce qui dans bien des cas est faux. Affiner le modèle va donc probablement passer au final par changer sa définition même.
Pour terminer
En début d’article nous avons créé un dataframe arbitraire sejours_du_jour.
Il faut savoir qu’il est tout à fait possible de prédire une valorisation de ces séjours de la même façon que pour sejours en précisant que nous allons appliquer le modèle entrainé sur sejours aux données de sejours_du_jour :
# On va utiliser m4 (mais vous pouvez choisir celui de votre choix)
# Pour rappel m4 est défini par
> m4 <- lm(valorisation ~ ds_classe + type_sejour, data = sejours)
# data= vaut "sejours" car là on entraine le modèle
# On peut produire une prédiction sur de nouvelles données grâce au
# paramètre "newdata=" car là on l'interroge sur d'autres données:
> predict(m4, newdata = sejours_du_jour)
1 2
1077.129 7617.566
# Ce qui peut s'inclure dans une chaine de traitement dplyr ainsi :
> sejours_du_jour %>%
mutate(valorisation = predict(m4, newdata = .))
# A tibble: 2 × 5
NO_ADMIN ds type_sejour ds_classe valorisation
<dbl> <dbl> <chr> <fct> <dbl>
1 1 0 HTP [0,2) 1077.
2 100 10 HC [10,30) 7618.Nous obtenons ainsi une colonne supplémentaire dans sejours_du_jour qui a prédit la valorisation en se basant sur l’expérience acquise en traitant sejours. Je vous laisse essayer par exemple en prenant d’un côté votre visualvalo d’un mois M pour l’entrainement et les nouveaux séjours du mois M+1 pour les prédire.
Conclusion
Un modèle simple, imparfait mais explicable, peut être plus utile qu’un modèle plus adapté mais opaque. Ici ces modèles simplifiés permettent d’avoir avant que le codage ne soit fait un indice sur leur valorisation.
En formalisant des raisonnements déjà connus des DIM, R permet de :
- rendre ces raisonnements reproductibles,
- les partager,
- et les discuter objectivement.
C’est souvent le premier pas vers des approches plus avancées. Ces dernières peuvent être plus performantes mais souvent au prix d’une interprétabilité inférieure (et donc peu accessible à la vulgariastion1). A l’occasion nous revisiterons la démarche du présent article avec un de ces modèles de ML mais pas tout de suite car j’ai eu des demandes hors IA que je voudrais aborder pour la prochaine fois. Mais rassurez-vous, l’IA va revenir !
- Pour la petite histoire, le présent article est en cours de rédaction depuis cet été et a été totalement réécrit au moins 4 fois car j’ai eu énormément de mal à limiter le niveau de technicité pour le garder accessible au plus grand nombre.
Il ignore volontairement de nombreux points conceptuels (la pertinence de l’estimation linéaire, l’utilisation de R2 pour évaluer l’erreur, la gestion différenciée des données catégorielles et numériques continues), d’implémentation informatique ou simplement des modèles que je sais plus efficaces mais inutilisables pour illustrer le sujet car trop opaques. ↩︎

